Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

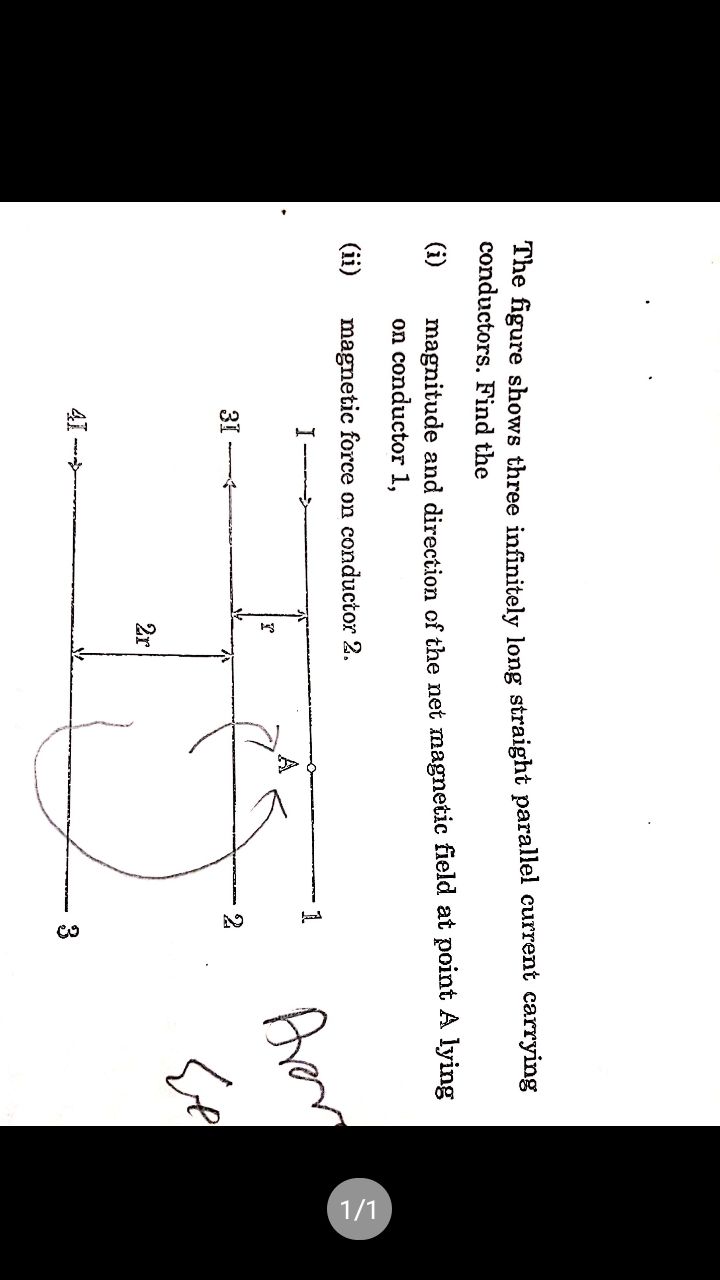
Parallel conductors 
question image
Asked by alanpeter9611 | 14 Feb, 2019, 05:21: PM
answered-by-expert Expert Answer

Cartesian coordinate system is shown in figure to represent the direction of magnetic field at a given point.
 
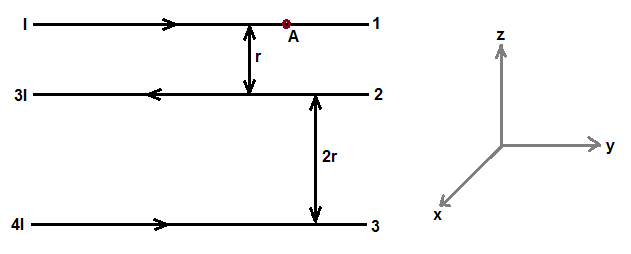
Magnetic field at A is due to current flow in conductor-2 and coductor 3.
 
In conductor-2 , current flow in -ve y direction.
If we apply right hand rule, we get magnetic fieldat A due to flow of current 3I in conductor 2 = 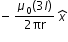begin mathsize 12px style negative space fraction numerator mu subscript 0 open parentheses 3 I close parentheses over denominator 2 πr end fraction space x with hat on top end style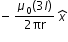.....................(1)
we get magnetic fieldat A due to flow of current 4I in conductor 3 = 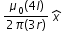begin mathsize 12px style space fraction numerator mu subscript 0 open parentheses 4 I close parentheses over denominator 2 pi open parentheses 3 r close parentheses end fraction space x with hat on top end style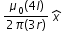........................(2)
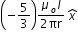
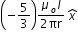
By adding eqn.(1) and eqn.(2), we get net magnetic field at A = begin mathsize 12px style open parentheses negative 5 over 3 close parentheses fraction numerator mu subscript o I over denominator 2 πr end fraction space x with hat on top end style
magnetic force on conductor-2 = B×i×L ,   where B is magnetic field on conductor-2, i is the current flowing in conductor-2
and L is the length of conductor-2
 
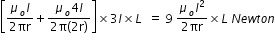
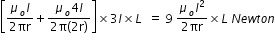
magnetic force = B×i×L = begin mathsize 12px style open square brackets fraction numerator mu subscript o I over denominator 2 πr end fraction plus fraction numerator mu subscript o 4 I over denominator 2 straight pi open parentheses 2 straight r close parentheses end fraction close square brackets cross times 3 I cross times L space space equals space 9 space fraction numerator mu subscript o I squared over denominator 2 πr end fraction cross times L space N e w t o n end style
Answered by Thiyagarajan K | 14 Feb, 2019, 11:11: PM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Physics
A dumbbell consists of two masses A and B each of mass m joined by a light rod of length l with mass B attached to a suspension point O by a light rod of length l as shown in figure. Find the minimum required speed with which mass A to be projected horizontally so that the system completes the vertical circular motion.
question image
Asked by artabandhusahu85 | 24 Apr, 2024, 12:07: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
What is charge?
Asked by niharvijayvargiya5 | 23 Apr, 2024, 06:40: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
please resolve with good explanation
question image
Asked by kulhariabhijeet | 21 Apr, 2024, 02:39: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
what are ghost particles please answer how is that not able to interact with other subatomic particles ..?is that faster than photons?
Asked by mohapatraswetalina88 | 21 Apr, 2024, 12:18: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
if breakdown voltage of each capacitor is 40v ,then maximum applied voltage Vmax will be
Asked by aishaisha091098 | 19 Apr, 2024, 04:54: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
explain
question image
Asked by ranadeb8090 | 19 Apr, 2024, 03:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
solve option e
question image
Asked by dasrituparna1999 | 13 Apr, 2024, 06:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
The number of moles in an elemental sample is just the ratio of the mass m to atomic mass 4. n= A The number of protons N, in an elemental sample is Z (atomic number) times the number of moles of Avogadro's number NA N=ZnN P A Copper has an atomic mass of 63.5 g/mole and 29 protons per atom. If such an atom were neutral, then it would have as many protons as electrons. If you remove electrons from a neutral state, then you get a net positive charge. Given a 54 gram ball of copper with a net charge of 2.2 µC, what fraction of the copper's electrons have been removed?
Asked by dasrituparna1999 | 12 Apr, 2024, 09:26: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
which answer is correct and most appropriate with explanation
question image
Asked by mishrigupta19319 | 08 Apr, 2024, 06:28: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
8212
question image
Asked by madhav9119887644 | 07 Apr, 2024, 08:10: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×