PA AND PB ARE ARE TWO TANGENTS DRAWN FROM AN EXTERNAL POINT TO A CIRCLE WITH CENTRE O [ALPHABET].. PROVE THAT OP IS THE RIGHT BISECTOR OF LINE SEGMENT AB
Asked by Anirudh
| 27th Nov, 2017,
06:22: PM
Expert Answer:
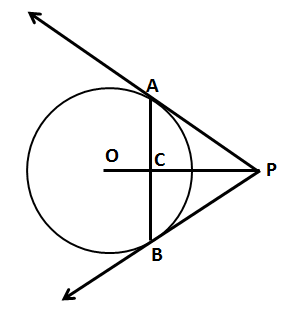
Answered by Rashmi Khot
| 27th Nov, 2017,
08:24: PM
Application Videos
Concept Videos
- in the given figure a triangle abc is drawn to circumscribe a circle of radius 3 cm such that the segment bd and dc are respectively of length 6 and 9 cm
if the area of traingle abc is 54cm2 then find side ab and ac
- prime factorisation
- prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact
- radious of circle is
- A tangent PQ at a point P on a circle of radius 5cm meets a line through the centre O at a point such that OQ=13cm. Find the length of PQ.
- Prove that the lengths of tangents drawn from an external point to a circle are equal. *
- The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. The radius of the circle is
- From any point on the common chord of two intersecting circles, tangents be drawn to thecircles, prove that they are equal.
- please answer these questions
- A tangent PA is drawn fron an external point P to a circle of radius 3
cm such that the distance of the point P from O is 6cm.Find yhe value of
.
Kindly Sign up for a personalised experience
- Ask Study Doubts
- Sample Papers
- Past Year Papers
- Textbook Solutions
Sign Up
Verify mobile number
Enter the OTP sent to your number
Change