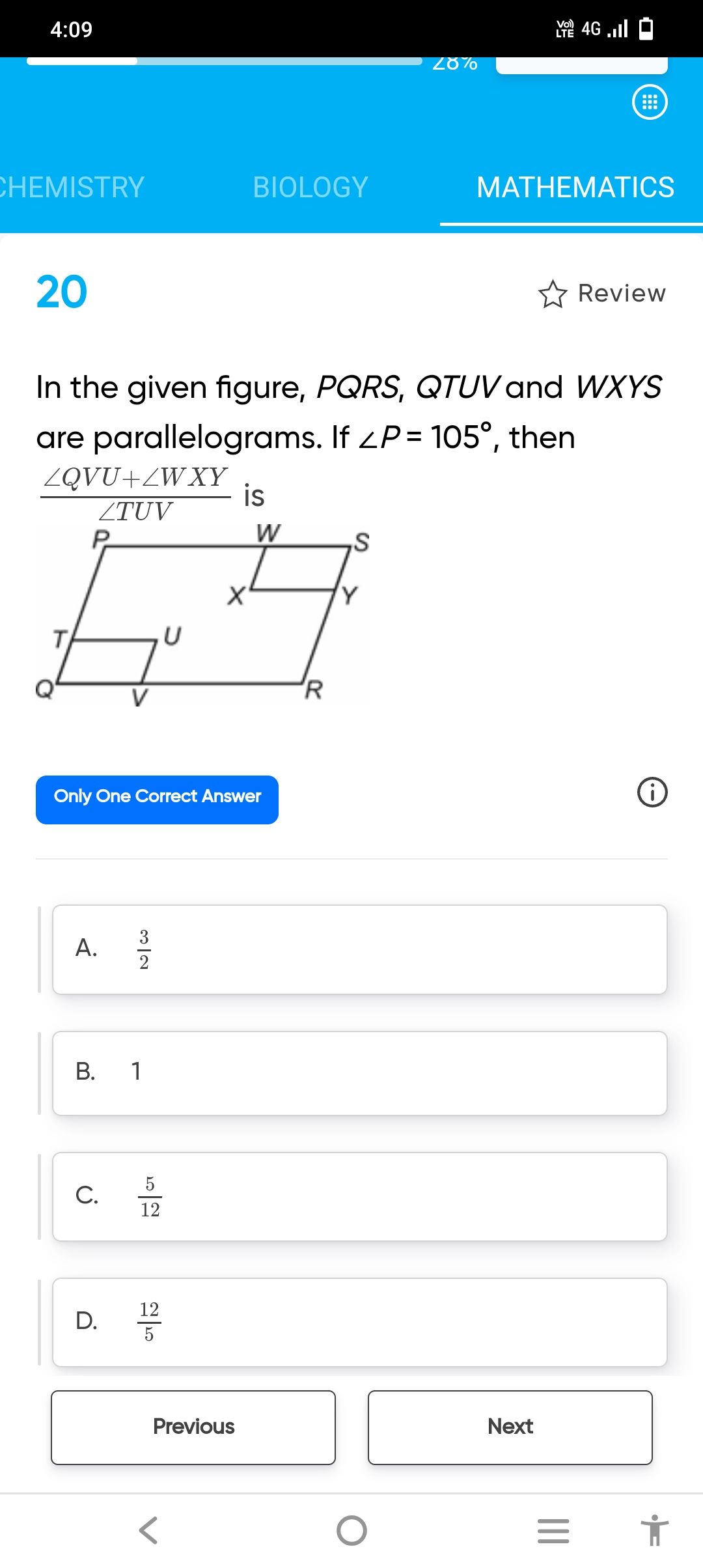
CBSE Class 9 Answered

Draw a circle with center O. And then, draw a rhombus OPQR inside the circle such that its one vertice lies on the center of the circle and the other 3 lie on the circumference of the circle. 

The diagonal OQ would split the triangle in 2 congruent triangles. Moreover, we can prove that triangles OPQ and ORQ are equilateral (with each side equal to radius).

We know that one diagonal of the rhombus = OQ = r

The length of other diagonal = 2 * altitude of the equilateral triangle ORQ = root 3 * r

Now area of rhombus with diagonals d1 and d2 = 1/2. d1 * d2

Hence, (1/2). r . root 3 * r = Area

Since r = 12cm

Hence, area = root(3)/2 *12*12 = 72 root(3) cm^2