CBSE Class 11-science Answered
Obtain an expression for the difference in pressure inside a saop bubble floating in air.
Asked by seeni2005 | 19 Nov, 2021, 12:47: PM
Expert Answer
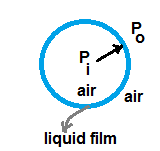
Suppose a spherical bubble of radius r, floating in air, is in equilibrium as shown in figure.
If its radius increase by Δr, then extra surface energy is
[4π(r + Δr) 2- 4πr2] T = 8πr Δr T ...........................(1)
Where T is surface tension. If the bubble is in equilibrium this energy cost is balanced by the energy gain due to
expansion under the pressure difference (Pi – Po) between the inside of the bubble and the outside.
The work done is
W = (Pi – Po) 4πr2Δr ...........................(2)
By equating the surface energy given by eqn.(1) and workdone as in eqn.(2) , we get
(Pi – Po) = (2 T ) / r
In general, for a liquid-gas interface, the convex side has a higher pressure than the
concave side. In the case of air bubble floating in air , we have two liquid-air interfaces , one inside the bubble and
another in outside of bubble .
(Pi – Po) = (4 T ) / r
Answered by Thiyagarajan K | 19 Nov, 2021, 09:01: PM
CBSE 11-science - Physics
Asked by vanshraaj.ind | 13 Dec, 2020, 06:06: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by Vidushi412 | 20 Dec, 2018, 12:23: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by Topperlearning User | 01 Aug, 2014, 01:26: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by Topperlearning User | 01 Aug, 2014, 01:27: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by Topperlearning User | 01 Aug, 2014, 01:32: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by Topperlearning User | 01 Aug, 2014, 01:42: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by Topperlearning User | 01 Aug, 2014, 02:01: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
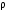coalesce to form single drop. The energy released in the processes is converted into kinetic energy. Find the speed of drop.Asked by Topperlearning User | 01 Aug, 2014, 03:03: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by Topperlearning User | 01 Aug, 2014, 03:43: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by Topperlearning User | 01 Aug, 2014, 03:46: PM
ANSWERED BY EXPERT
