Mathematically  prove that the total mechanical energy of a freely falling body is constant at all positions .

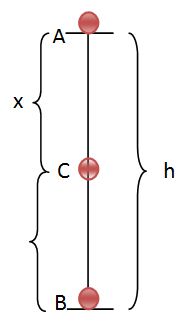
Let us consider an object of mass, ‘m’ is thrown upwards to a height ‘h’ above the ground level.

At point A:

The body must be at rest and v = 0

PE_A = mgh and KE_A = 0 

Total energy = PE_{A +}  KE_A = mgh ......... (Equation 1)

When the body drops down, let us say it covers a distance ‘x’ at point C. Thus, its height from the ground is ‘h – x’.

At point C:

PE_C = mg(h-x) = mgh – mgx  ........ (Equation 2)

At point B:

The body hits the ground u = 0 and h = 0

So, it possesses only kinetic energy.

PE_A = 0 

Thus, from equation (1), (5) and (7) that the total energy remains constant.