lET X BE RATIONAL AND Y BE IRRATIONAL.iS XY NECESSARILY IRRATIONAL?GIVE REASONS AND JUSTIFY WITH EXAMPLE?
Asked by raoss1967
| 6th May, 2015,
12:48: PM
Expert Answer:
Yes. The product of one rational and one irrational number is an irrational number.
It can be proved by method of contradiction.
Let X be a rational number such that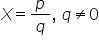 
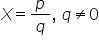
Y is an irrational number such that XY=R , a rational number, where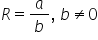 
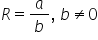
So we get
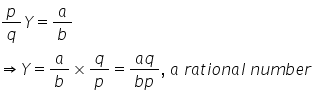
The above conclusion is a contradiction, since Y is an irrational number.
Hence, our initial assumption that XY is rational is not true. Hence, XY is irrational. Proved.
For example, suppose X=3 and Y=√2 . XY=3√2 which is an irrational number.
Answered by satyajit samal
| 7th May, 2015,
04:48: PM
Concept Videos
- what is rational number
- ✓500 root
- show that 2+√5 is an irrational number
- prove that root5 is an irrational number
- find the lcm of20
- WHat are rational numbers?
- i dont know how to solve logarithms could any one have grip on logarithm pls reply me
- √324is whose no.
- prove that 5 root is irrational
- what are real roots?
Kindly Sign up for a personalised experience
- Ask Study Doubts
- Sample Papers
- Past Year Papers
- Textbook Solutions
Sign Up
Verify mobile number
Enter the OTP sent to your number
Change