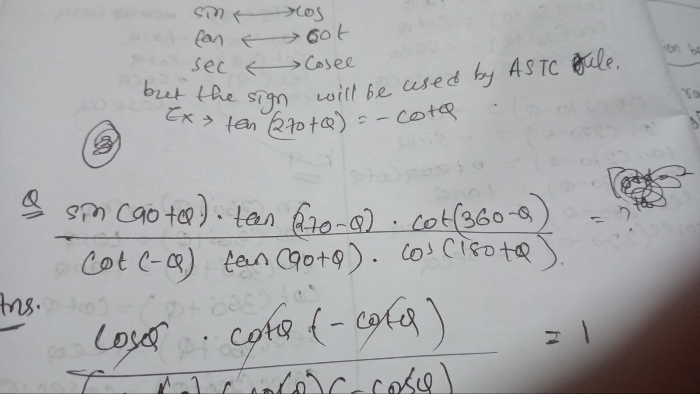CBSE Class 11-science Answered
Let PQ and RS be two parallel chords of a given circle of radius 6 cm lying on the same side of the centre. If the chords subtends angles of 72? and 144? at the centre and the distance between the chords is d, then find the value of (d square).
Asked by samiddhamukherjee | 16 Sep, 2010, 11:50: PM
Dear Student,
Let the distance of the nearer chord from the center be X cm. Therefore the distance of the farther chord is X + d cm.
From the figure we get,
cos(36o) = (X + d)/6 ---------(1)
and
cos(72o) = (X)/6 ---------(2)
From (2) we get,
X = 6cos(72o)
Putting this value in (1) we get
6cos(36o) = 6cos(72o) + d
=> d = 6(cos(36o) - cos(72o))
Calculating the value of cos(36o) and cos(72o) from trigonometric ratios table, we get
cos(360) = 0.809
cos(72o) = 0.309
=> d = 6(0.809 - 0.309)
=> d = 6 x 0.5
=> d = 3.
Regards Topperlearning.
Answered by | 17 Sep, 2010, 12:33: AM
Concept Videos
CBSE 11-science - Maths
Asked by rajyothi64 | 05 Mar, 2024, 09:49: PM
CBSE 11-science - Maths
Asked by ghoshshawata62 | 04 Mar, 2024, 08:16: PM
CBSE 11-science - Maths
Asked by nayaktapaswini2007 | 29 Feb, 2024, 09:10: AM
CBSE 11-science - Maths
Asked by bimanmandal53361 | 15 Jan, 2024, 12:32: AM
CBSE 11-science - Maths
Asked by sreyas.katuri | 23 Sep, 2023, 07:12: AM
CBSE 11-science - Maths
Asked by 069.pks | 16 Sep, 2023, 10:06: AM
CBSE 11-science - Maths
Asked by surekhashriwas01 | 12 Sep, 2023, 08:39: PM
CBSE 11-science - Maths
Asked by mvr23467 | 12 Sep, 2023, 07:52: PM
CBSE 11-science - Maths
Asked by SasipriyaNagappan | 27 Jul, 2023, 07:22: PM