Let G be the centroid of triangle ABC if AB bar=a bar AC bar=b bar then the bisector AG bar in terms of a bar and b bar is

CBSE Class 12-science Answered

Let G be the centroid of triangle ABC if AB bar=a bar AC bar=b bar then the bisector AG bar in terms of a bar and b bar is

Asked by Kalyanrao Chavan | 23 Jun, 2014, 10:07: PM

Expert Answer

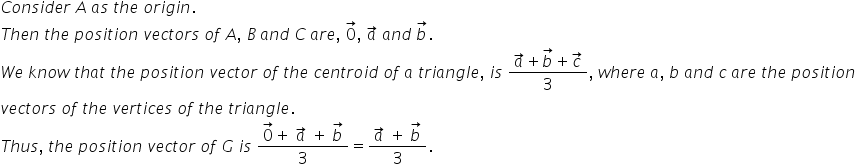
C o n s i d e r space A space a s space t h e space o r i g i n. T h e n space t h e space p o s i t i o n space v e c t o r s space o f space A comma space B space a n d space C space a r e comma space 0 with rightwards arrow on top comma space a with rightwards arrow on top space a n d space b with rightwards arrow on top. W e space k n o w space t h a t space t h e space p o s i t i o n space v e c t o r space o f space t h e space c e n t r o i d space o f space a space t r i a n g l e comma space i s space fraction numerator a with rightwards arrow on top plus b with rightwards arrow on top plus c with rightwards arrow on top over denominator 3 end fraction comma space w h e r e space a comma space b space a n d space c space a r e space t h e space p o s i t i o n v e c t o r s space o f space t h e space v e r t i c e s space o f space t h e space t r i a n g l e. T h u s comma space t h e space p o s i t i o n space v e c t o r space o f space G space i s space fraction numerator 0 with rightwards arrow on top plus space a with rightwards arrow on top space plus space b with rightwards arrow on top over denominator 3 end fraction equals fraction numerator a with rightwards arrow on top space plus space b with rightwards arrow on top over denominator 3 end fraction.

Answered by Vimala Ramamurthy | 24 Jun, 2014, 10:14: AM

Answered Unanswered My Questions My Answers

CBSE 12-science - Maths

Asked by mohdtayyab682 | 18 Jan, 2023, 10:34: PM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Plz asnwer 15 (ii)part

Asked by lovemaan5500 | 07 Feb, 2020, 09:49: AM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Asked by Vivek.d8765 | 29 Oct, 2019, 10:14: PM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Define unit vector.