Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

Let f(x)=2008x+2008-x/2, g(x)= 2008x-2008-x/2 then prove that f(x+y)=f(x)f(y)+g(x)g(y).

Asked by Anil | 11 May, 2017, 12:13: PM
answered-by-expert Expert Answer
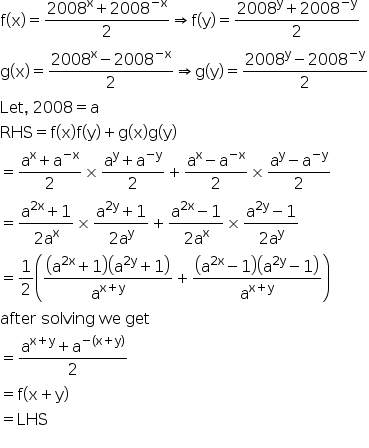
begin mathsize 16px style straight f open parentheses straight x close parentheses equals fraction numerator 2008 to the power of straight x plus 2008 to the power of negative straight x end exponent over denominator 2 end fraction rightwards double arrow straight f open parentheses straight y close parentheses equals fraction numerator 2008 to the power of straight y plus 2008 to the power of negative straight y end exponent over denominator 2 end fraction straight g open parentheses straight x close parentheses equals fraction numerator 2008 to the power of straight x minus 2008 to the power of negative straight x end exponent over denominator 2 end fraction rightwards double arrow straight g open parentheses straight y close parentheses equals fraction numerator 2008 to the power of straight y minus 2008 to the power of negative straight y end exponent over denominator 2 end fraction Let comma space 2008 equals straight a RHS equals straight f open parentheses straight x close parentheses straight f open parentheses straight y close parentheses plus straight g open parentheses straight x close parentheses straight g open parentheses straight y close parentheses equals fraction numerator straight a to the power of straight x plus straight a to the power of negative straight x end exponent over denominator 2 end fraction cross times fraction numerator straight a to the power of straight y plus straight a to the power of negative straight y end exponent over denominator 2 end fraction plus fraction numerator straight a to the power of straight x minus straight a to the power of negative straight x end exponent over denominator 2 end fraction cross times fraction numerator straight a to the power of straight y minus straight a to the power of negative straight y end exponent over denominator 2 end fraction equals fraction numerator straight a to the power of 2 straight x end exponent plus 1 over denominator 2 straight a to the power of straight x end fraction cross times fraction numerator straight a to the power of 2 straight y end exponent plus 1 over denominator 2 straight a to the power of straight y end fraction plus fraction numerator straight a to the power of 2 straight x end exponent minus 1 over denominator 2 straight a to the power of straight x end fraction cross times fraction numerator straight a to the power of 2 straight y end exponent minus 1 over denominator 2 straight a to the power of straight y end fraction equals 1 half open parentheses fraction numerator open parentheses straight a to the power of 2 straight x end exponent plus 1 close parentheses open parentheses straight a to the power of 2 straight y end exponent plus 1 close parentheses over denominator straight a to the power of straight x plus straight y end exponent end fraction plus fraction numerator open parentheses straight a to the power of 2 straight x end exponent minus 1 close parentheses open parentheses straight a to the power of 2 straight y end exponent minus 1 close parentheses over denominator straight a to the power of straight x plus straight y end exponent end fraction close parentheses after space solving space we space get equals fraction numerator straight a to the power of straight x plus straight y end exponent plus straight a to the power of negative open parentheses straight x plus straight y close parentheses end exponent over denominator 2 end fraction equals straight f open parentheses straight x plus straight y close parentheses equals LHS end style
Answered by Sneha shidid | 11 May, 2017, 05:02: PM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Maths
Find the range and domain of the following function :- f(x) = | x^2 - 1 |
question image
Asked by suryansh141107 | 16 Oct, 2023, 09:29: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
|x|³-7|x|+6=0 pls solve with modulus
Asked by sohammukherjee0007 | 04 Oct, 2023, 11:01: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
find relation between x,y and z x² + 4y² + 9z² - 2xy - 3xz - 6yz = 0
Asked by sundramsingh1707 | 11 Jun, 2022, 05:20: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
If f(x) = ex and g(x) = loge x then the value of fog(1) is
Asked by maarcusfelix2006 | 24 Jul, 2021, 07:39: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the equation of the locus which is at 5 units distance from the point A(3,_2)
Asked by Jagannadhameshwar5 | 15 Jul, 2021, 09:17: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Hello sir I need a full explanation of this sum find domain and range of f(x)=|2x-3|-3
Asked by seeni2005 | 12 Oct, 2020, 08:50: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Please help to solve  
question image
Asked by jasi01f4 | 06 Oct, 2020, 11:02: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Hello sir, Please explain this sum, Find the domain of the functions i) f(x) = 1/√(x^2 -5x + 6)  ii) f(x) = x^2+2x+1/x^2-8x+12
Asked by seeni2005 | 21 Sep, 2020, 03:04: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
4x+1 then x =
Asked by rajvirsinhzala16 | 14 Aug, 2020, 12:43: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
mod(2x-[x])=4 where [] represent greatest integer function  
Asked by hrishityelchuri2017 | 19 May, 2020, 09:58: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×