Let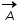 
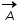be vector parallel to the line of intersection of planes P1 and P2. Plane P1 is parallel to the
vectors 2j^ +3k^ and 4j^ - 3k^ and plane P2 is parallel to j^- k^ and 3i^ + 3j^ . Find the angle
between the vector 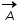and a given vector 2i^ + j^ - 2k^
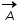be vector parallel to the line of intersection of planes P1 and P2. Plane P1 is parallel to the and a given vector 2i^ + j^ - 2k^
Asked by ahuja8087
| 14th Feb, 2017,
07:22: PM
Expert Answer:
Answered by Rebecca Fernandes
| 15th Feb, 2017,
09:54: AM
Concept Videos
Q 48
- If
is the normal from the origin to the plane, and 
is the unit vector along . P(x, y, z) be any point on the plane and 
is perpendicular to . Find the equation of plane in the normal form.
- Let
be the vector normal to the plane and 
be the position vector of the point through which the plane passes. Then find the equation of plane.
- Find the equation of the plane, which is at a distance of 5 unit from the origin and has
as a normal vector.
- Find the equation of the plane whose distance from the origin is 8 units and the direction ratios of the normal are 6, – 3, – 2.
- Find the equation of the plane is
. Find the perpendicular distance of the plane from the origin.
- Write the normal and Cartesian form of the plane
.
- Find the equation of the plane passing through the points (–1, 4, – 3), (3, 2, – 5) and (– 3, 8, – 5).
- Find the equation of the plane passing through the point (3, – 3, 1) and perpendicular to the line joining the points (3, 4, – 1) and (2, – 1, 5).
- Find the co-ordinates of the foot of the perpendicular drawn from the origin to the plane 2x – 3y + 6z + 7 = 0.
Kindly Sign up for a personalised experience
- Ask Study Doubts
- Sample Papers
- Past Year Papers
- Textbook Solutions
Sign Up
Verify mobile number
Enter the OTP sent to your number
Change