Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

Let 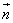 be the vector normal to the plane and  be the position vector of the point through which the plane passes. Then find the equation of plane.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
answered-by-expert Expert Answer

Let P be a arbitrary point on the plane with position vector .

 
 
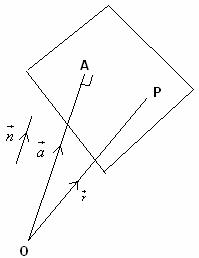
Thus, equation of the plane with 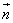 as a normal vector and  as a position vector of the point through which the plane passes is
 
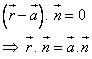
Answered by | 04 Jun, 2014, 03:23: PM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Maths
Q 48
question image
Asked by lekhakarthikeyan | 16 Jul, 2018, 03:58: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
If  is the normal from the origin to the plane, and  is the unit vector along . P(x, y, z) be any point on the plane and  is perpendicular to . Find the equation of plane in the normal form.
Asked by Topperlearning User | 26 Feb, 2015, 10:10: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Let  be the vector normal to the plane and  be the position vector of the point through which the plane passes. Then find the equation of plane.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the equation of the plane, which is at a distance of 5 unit from the origin and has as a normal vector.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the equation of the plane whose distance from the origin is 8 units and the direction ratios of the normal are 6, – 3, – 2.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the equation of the plane is . Find the perpendicular distance of the plane from the origin.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Write the normal and Cartesian form of the plane .
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the equation of the plane passing through the points (–1, 4, – 3), (3, 2, – 5) and (– 3, 8, – 5).
Asked by Topperlearning User | 26 Feb, 2015, 10:50: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the equation of the plane passing through the point (3, – 3, 1) and perpendicular to the line joining the points (3, 4, – 1) and (2, – 1, 5).
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the co-ordinates of the foot of the perpendicular drawn from the origin to the plane 2x – 3y + 6z + 7 = 0.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×