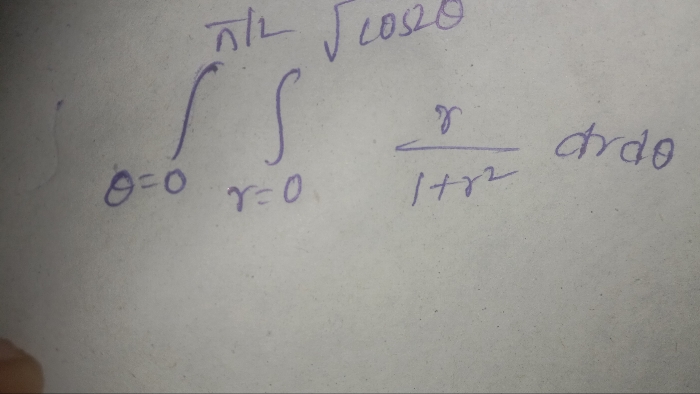CBSE Class 12-science Answered
Integate the following- Sec2x/(secx+tanx)9/2
Asked by Satendra Pal | 02 Nov, 2012, 05:39: PM
Let secx + tanx = t .............. [1]
thus, { secx - tanx } = 1 / t .....[2]
solving , 1 & , 2 , we get,
secx = t2 + 1 / 2t .....[3]
Now , again consider secx + tanx = t
Differentiating both sides , with respect to 'x ' , we get,
secx* tanx + sec2 x = dt / dx
secx { secx + tanx } = dt / dx
secx { t } = dt/ dx ... ..[4]
putting the value of secx from [3] in [4], we get,
dx = dt * 2 / [ t2 + 1 ]
Now, put the value of t to get the answer.
Answered by | 02 Nov, 2012, 05:51: PM
Concept Videos
CBSE 12-science - Maths
Asked by jprathamesh023 | 23 Mar, 2024, 04:01: PM
CBSE 12-science - Maths
Asked by atulmishra514 | 26 Jan, 2024, 10:15: PM
CBSE 12-science - Maths
Asked by aalavarshitha2005 | 21 Jan, 2024, 05:28: PM
CBSE 12-science - Maths
Asked by atharvaparkar04 | 17 Dec, 2023, 12:59: PM
CBSE 12-science - Maths
Asked by shashinayaka032 | 05 Dec, 2023, 12:46: PM
CBSE 12-science - Maths
Asked by manyarajawat1 | 06 Nov, 2023, 05:03: PM
CBSE 12-science - Maths
Asked by ps9680677 | 26 Oct, 2023, 11:47: AM
CBSE 12-science - Maths
Asked by manasvichandel49 | 19 Oct, 2023, 08:53: AM