Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

In two concentric circles the radius of inner is 5 cm a chord of length 24 m of outer circle becomes a tangent to the inner circle. Find the radius of the larger circle.
Asked by Topperlearning User | 27 Jul, 2017, 01:04: PM
answered-by-expert Expert Answer

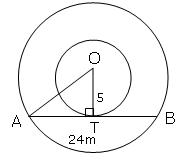
Let O be the centre of circle and AB be the chord OT is radius of smaller circle

So OTAB since tangent is to radius at its point of contact.

AT = TB = 12 cm

(since perpendicular from centre to the chord bisects it)

So, In triangle OAT,

OA2 = OT2 + AT2

OA2 = 52 + 122

So, OA = 13 cm

Thus, the radius of the larger circle is 13 cm.

 

Answered by | 27 Jul, 2017, 03:04: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
in the given figure a triangle abc is drawn to circumscribe a circle of radius 3 cm such that the segment bd and dc are respectively of length 6 and 9 cm if the area of traingle abc is 54cm2 then find side ab and ac
question image
Asked by jennyy | 26 Mar, 2022, 08:41: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
prime factorisation
Asked by amikasangma080 | 11 Oct, 2021, 06:14: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact
Asked by muskanmahek2411 | 08 Oct, 2021, 10:48: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
radious of circle is
Asked by anishasheoran372 | 13 Jul, 2021, 09:33: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
A tangent PQ at a point P on a circle of radius 5cm meets a line through the centre O at a point such that OQ=13cm. Find the length of PQ.
Asked by anushkasingh260805 | 20 Dec, 2020, 07:22: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Prove that the lengths of tangents drawn from an external point to a circle are equal. *
Asked by anjalirajp004 | 22 Sep, 2020, 08:17: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. The radius of the circle is
Asked by rashikediadelhi | 21 Sep, 2020, 09:02: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
From any point on the common chord of two intersecting circles, tangents be drawn to thecircles, prove that they are equal. 
Asked by prasutally | 26 May, 2019, 08:23: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
please answer these questions
question image
Asked by prasutally | 26 May, 2019, 08:22: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
A tangent PA is drawn fron an external point P to a circle of radius 3 square root of 2cm such that the distance of the point P from O is 6cm.Find yhe value ofangle A p o. 
Asked by kamatshantanu | 08 May, 2019, 11:39: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×