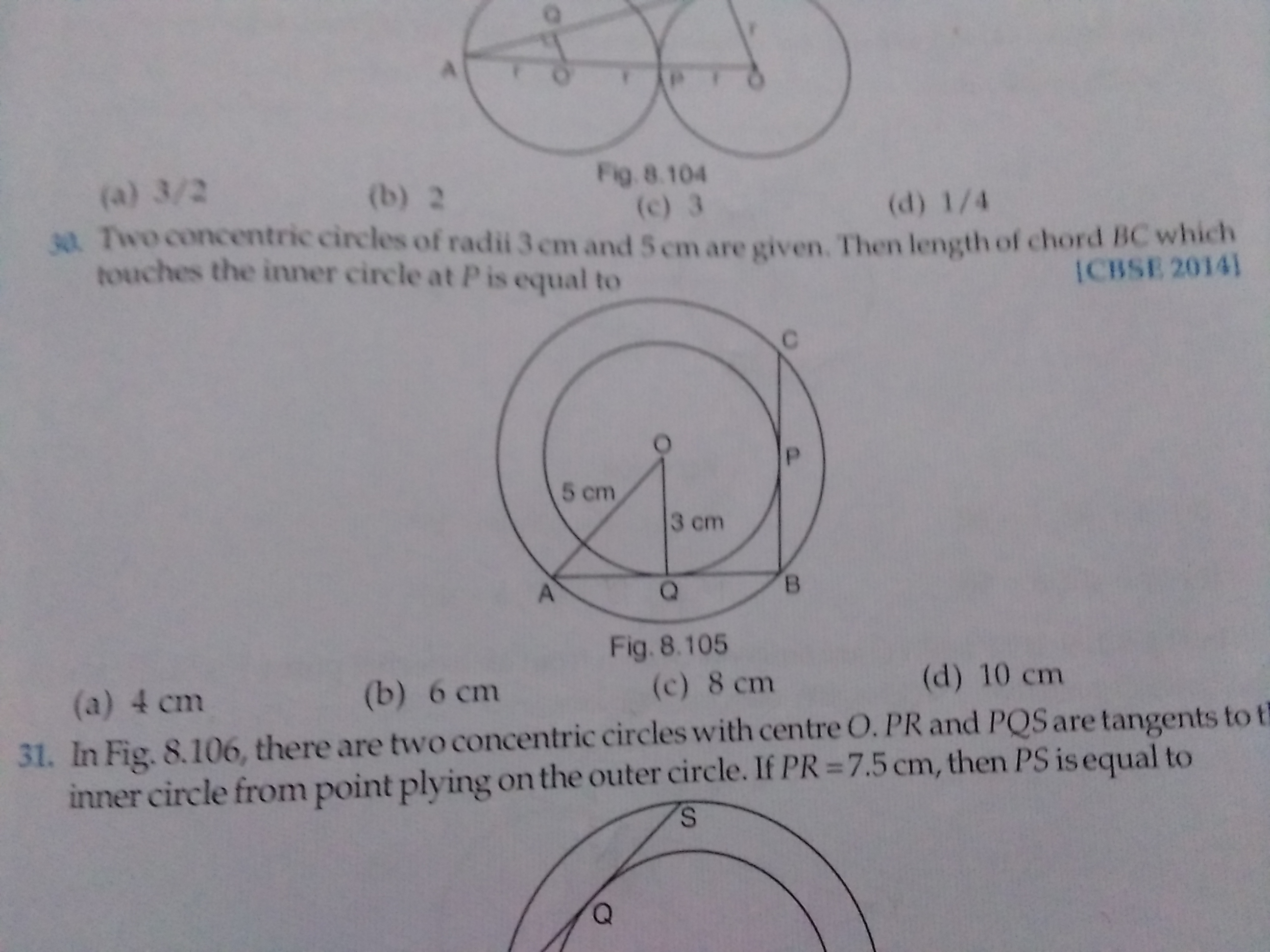
In two concentric circles,prove that chords of the outer circle which touch the inner are of equal length.

Dear student

chords of the outer circle which touch the inner circle will be tangents to the inner circle and tangent is perpendicular to the radius at its point of contact so these chords are at the distance equal to the radii of inner circle from the centre of outer circle

Hence the chords are equidistant from the centre and therefore equal in length using the result the chords equidistant from the centre are equal in length

Regards

Team Topper