ICSE Class 9 Answered
In triangle ABC the bisector of angle ABC and ACB meet at O.If OB=OC prove that triangle ABC is an isosceles triangle.
Asked by rkarim957 | 14 Jul, 2019, 11:53: AM
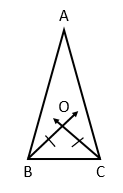
Given : Triangle OBC is an isosceles triangle. BO and CO are the bisectors of angle B and angle C.
To prove : triangle ABC is an isosceles
Proof :
In triangle OBC,
OB = OC
angle OBC = angle OCB opposite angles of equal sides
angle AOB = angle OBC .....(i)
and angle ACO = angle OCB ....(ii)
Adding (i) and (ii) we get
angle AOB + angle ACO = angle OBC + angle OCB
angle ABC = angle ACB
AB = AC opposite sides of an equal angles
Hence, triangle ABC is an isosceles triangle.
Answered by Sneha shidid | 15 Jul, 2019, 10:14: AM
Application Videos
Concept Videos
ICSE 9 - Maths
Asked by alonesuvam.123 | 27 Dec, 2023, 08:40: PM
ICSE 9 - Maths
Asked by dola2408m | 04 Sep, 2021, 03:27: PM
ICSE 9 - Maths
Asked by sheetalgoel25 | 19 Oct, 2020, 06:11: PM
ICSE 9 - Maths
Asked by chsrvsh | 24 Jul, 2019, 09:29: PM
ICSE 9 - Maths
Asked by rkarim957 | 14 Jul, 2019, 11:53: AM
ICSE 9 - Maths
Asked by evangelinexess393 | 02 Jan, 2018, 03:09: PM