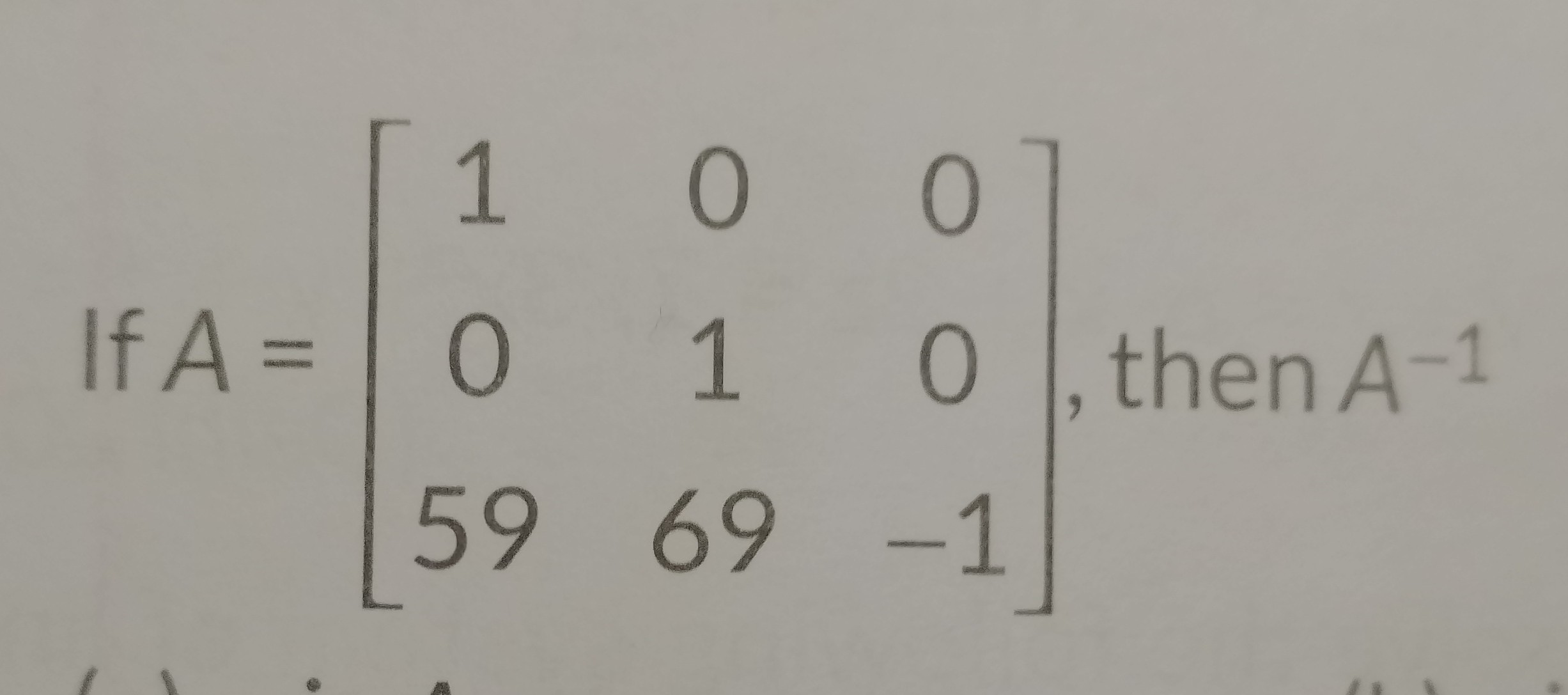Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

in this topic when we apply ele. row operation we write A = IA and for column A = AI . but we are confuse this concept . Can we write AAinverse = I for both the operation.
Asked by jasbeer | 12 Apr, 2015, 02:17: AM
answered-by-expert Expert Answer
A=IA=AI is always true for a matrix A and an identity matrix I.
So, we can use A =IA or A=AI as per convenience.
A-1A=I is true for any matrix A. So we can write it for both the operations.
Answered by satyajit samal | 13 Apr, 2015, 06:11: PM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Maths
how to solve the adjoint of 3×3 matrix
question image
Asked by rahulsharmaaps4 | 03 Jan, 2023, 10:46: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Solve only by using elementary operations not Adjoints:
question image
Asked by Gounshi | 01 Jun, 2020, 05:07: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
An amont of 600 crores is spent by the Government in 3 Schemes (A,B,C). Now twice the amount spent on Scheme C together with the amount spent on Scheme A is Rs. 500 crores. Three times the amount spent on Scheme A together with the amount spent on Scheme B and Scheme C is Rs. 1200 crores.Find the amount spent on each scheme using matrices.Read more on Sarthaks.com - https://www.sarthaks.com/547624/an-amont-of-600-crores-is-spent-by-the-government-in-3-schemes-a-b-c
Asked by neerajnirupammohanty95 | 28 Apr, 2020, 10:15: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
find a^-1 using elementary row operation of  a=  open square brackets table row cell negative 1 end cell 2 1 row 1 2 3 row 3 1 3 end table close square brackets  
Asked by spd231624 | 04 May, 2019, 09:54: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
solve the following system of linear equations using matrix method 2x-y-z=7,3x+y-z=7,x+y-z=3  
Asked by prashubh2000 | 25 Apr, 2019, 11:31: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Solve by matrix method: 2x+y+2z=5, x-y-z=0, x+2y+3z=5.
Asked by ppgm11patil | 29 Oct, 2018, 02:21: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
find inverse of matrix using elementary row operation(ignore absence of bracket) 0   1     2 1   2     3 3   1     1
Asked by haroonrashidgkp | 31 Mar, 2018, 12:12: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
find inverse of matrx using elementary row operation (i)   1     2        2    -1 ii )    2      5        -3      1 ignore ithe absence of braclet and consider it in square bracket also sate the key method to find matrix
Asked by haroonrashidgkp | 26 Mar, 2018, 09:11: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Define invertible matrix with example.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find , if it exist, given
Asked by Topperlearning User | 29 Apr, 2016, 07:51: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×