Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 9 Answered

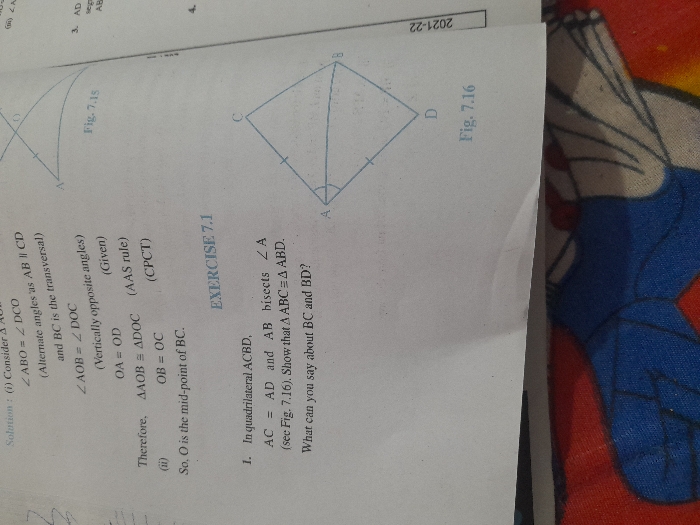
<div>In the given figure ,ABCD is a square and EF is parallel to diagnol DB and EM=FM.Prove that:(i)BF=DE,(ii)AM bisects angle BAD<img src="https://images.topperlearning.com/topper/tinymce/imagemanager/files/5eeded484f0aa9f8980f5fccfc1766f657c01c6a2fa394.86591791ART.png" alt="" /></div>
Asked by abinash.gupta003 | 26 Aug, 2016, 04:13: PM
Expert Answer
begin mathsize 14px style left parenthesis straight i right parenthesis In space triangle BCD comma space BC equals CD rightwards double arrow angle CBD equals angle CDB Also comma space EF space is space parallel space to space BD comma angle CEF equals angle CDB space and space angle CFE equals angle CBD space space space space left parenthesis corresponding space angles right parenthesis rightwards double arrow angle CEF equals angle CFE rightwards double arrow CE equals CF rightwards double arrow CD minus DE equals BC minus BF rightwards double arrow DE equals BF left parenthesis ii right parenthesis In space triangle ADE space and space triangle ABF comma AD equals AB angle ADE equals angle ABF space space space space space left parenthesis each space 90 degree right parenthesis DF equals BE space space space space space left parenthesis From space left parenthesis straight i right parenthesis right parenthesis So space triangles space ADE space and space ABF space are space similar space by space SAS space property rightwards double arrow AE equals AF space and space FM equals EM space left parenthesis given right parenthesis AM equals AM So space triangles space triangle AMF space and space triangle AME space are space similar space by space SSS space property rightwards double arrow angle FAM equals angle EAM rightwards double arrow angle FAM plus angle BAF equals angle EAM plus angle EAD rightwards double arrow angle DAM equals angle BAM rightwards double arrow AM space bisects space BAD end style
Answered by Rashmi Khot | 26 Aug, 2016, 05:08: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test Subjective Questions Webinar Subjective Questions Pre Board Assessment
Answered Unanswered My Questions My Answers
CBSE 9 - Maths
M is a point inside a square ABCD. AMCD is equilateral triangle and MC cuts diagonal DB at E. Then, ZBEC=..... (1) 75° (3) 105° (2) 90° (4) 60°
Asked by Krishna962511 | 23 Jan, 2023, 10:41: AM
ANSWERED BY EXPERT
CBSE 9 - Maths
prove that medians of a triangle are equal
Asked by kandalashyamala20 | 27 Dec, 2022, 02:30: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
the angles of a triangle are in the ratio of 2 :3:4
Asked by sumitrasangwa041 | 02 Jul, 2022, 02:21: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
answers
Asked by bathinisampath | 05 Apr, 2022, 10:52: AM
ANSWERED BY EXPERT
CBSE 9 - Maths
SAS congruence axiom is
Asked by bathinisampath | 05 Apr, 2022, 10:50: AM
ANSWERED BY EXPERT
CBSE 9 - Maths
In fig. 12.116 , T is a point on the side QR of ∆ PQR and S is a point such that RT=St. Prove that PQ+PR>QS
Asked by shivendrasinghfauzdar | 09 Oct, 2021, 11:30: AM
ANSWERED BY EXPERT
CBSE 9 - Maths
be and CF are two traiangle equal altitude of triangle abc using rhs congruence rule prove that the triangle abc is isosceles
Asked by arahant2008 | 07 Oct, 2021, 09:38: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
In the figure, ABCD is a square and PAB is a triangle such that AQ = BR. Prove that DPQR is an isosceles triangle.
Asked by thebeatinbrat | 01 Oct, 2021, 08:56: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
sir is two triangles is congurance by two properties
Asked by abdulsamad82007 | 15 Jun, 2021, 12:59: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
Q2. In ABC, AB = AC. X and Y are points on AB and AC such that AX = AY. Prove that ABY  ACX 
Asked by rjaat7623 | 28 Feb, 2021, 10:57: AM
ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get FREE Sample Mock Papers for Final Exams
Download Now
×