Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

iN THE FIG, THE COMMON TANGENT, AB AND CD TO TWO CIRCLES WITH CENRES O, AND O' INTERSECT AT E. PROVE THAT THE POINTS O, E, O' ARE COLLINEAR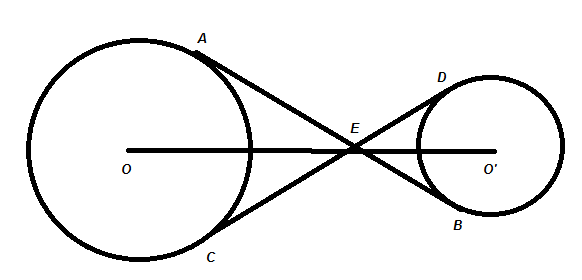
Asked by Divyaa | 25 Mar, 2017, 02:52: PM
answered-by-expert Expert Answer
begin mathsize 16px style Construction colon space Join space OA space and space OC. In space increment OAE space and space increment OCE comma space we space have OA equals OC space left parenthesis radii space of space the space same space circle right parenthesis OE equals OE space left parenthesis common space side right parenthesis angle OAE equals angle OCE space left parenthesis each space is space 90 degree right parenthesis rightwards double arrow increment OAE approximately equal to increment OCE space left parenthesis RHS space congruence space criterion right parenthesis rightwards double arrow angle AEO equals angle CEO space left parenthesis cpct right parenthesis Similarly comma space angle BEO apostrophe equals angle DEO apostrophe angle AEC equals angle DEB rightwards double arrow 1 half angle AEC equals 1 half angle DEB rightwards double arrow angle AEO equals angle CEO equals angle BEO apostrophe equals angle DEO apostrophe Since space these space angles space are space equal space and space are space bisected space by space OE space and space straight O apostrophe straight E comma space straight O comma space straight E space and space straight O apostrophe space are space collinear. end style
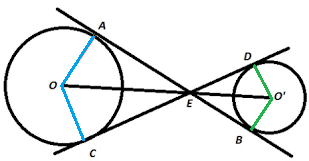
Answered by Rebecca Fernandes | 25 Mar, 2017, 05:39: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
in the given figure a triangle abc is drawn to circumscribe a circle of radius 3 cm such that the segment bd and dc are respectively of length 6 and 9 cm if the area of traingle abc is 54cm2 then find side ab and ac
question image
Asked by jennyy | 26 Mar, 2022, 08:41: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
prime factorisation
Asked by amikasangma080 | 11 Oct, 2021, 06:14: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact
Asked by muskanmahek2411 | 08 Oct, 2021, 10:48: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
radious of circle is
Asked by anishasheoran372 | 13 Jul, 2021, 09:33: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
A tangent PQ at a point P on a circle of radius 5cm meets a line through the centre O at a point such that OQ=13cm. Find the length of PQ.
Asked by anushkasingh260805 | 20 Dec, 2020, 07:22: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Prove that the lengths of tangents drawn from an external point to a circle are equal. *
Asked by anjalirajp004 | 22 Sep, 2020, 08:17: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. The radius of the circle is
Asked by rashikediadelhi | 21 Sep, 2020, 09:02: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
From any point on the common chord of two intersecting circles, tangents be drawn to thecircles, prove that they are equal. 
Asked by prasutally | 26 May, 2019, 08:23: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
please answer these questions
question image
Asked by prasutally | 26 May, 2019, 08:22: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
A tangent PA is drawn fron an external point P to a circle of radius 3 square root of 2cm such that the distance of the point P from O is 6cm.Find yhe value ofangle A p o. 
Asked by kamatshantanu | 08 May, 2019, 11:39: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×