CBSE Class 12-science Answered
In Rolls theorem f(x) is continuous on [a,b] but f(x) is differentiable on (a,b) my question is that why f(x) is not differentiable on [a,b] that is on closed interval.
Asked by Kalyanrao Chavan | 02 Aug, 2014, 10:11: PM

Answered by Vimala Ramamurthy | 04 Aug, 2014, 10:26: AM
Concept Videos
CBSE 12-science - Maths
Asked by agarwalgolu318 | 13 Aug, 2020, 08:09: PM
CBSE 12-science - Maths
Asked by givduf | 11 Jul, 2020, 09:00: AM
CBSE 12-science - Maths
Asked by sonalchoudhary882 | 22 Oct, 2018, 12:22: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 08:27: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 08:32: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 09:19: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 09:58: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 10:14: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 11 Aug, 2014, 10:06: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 12:43: PM




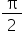 is
is