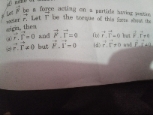Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

iN parallel axis theo MI=sigma m .sq(d+x) =sigma m.sq(d) +sigma m.sq(x) + 2d sigma(x) =m.sq(d) + Icg +0 why is 2d sigma(x)=0
Asked by timesnow | 21 Nov, 2010, 11:22: PM
answered-by-expert Expert Answer
Dear student
 
A/C parallel axis theorem,
 
I = Ig + Md2
 
 I = Σm ( x2 + d2 + 2dh)
      = Σmx2  + Σmd2    + Σ2mdh............(i)
 
Now if the body rotates about a given axis such that the chosen particle rotates in a circle of radius x;
 
Ig  = Σmx2
Σmd2 = d2 Σm = Md2
 
The term,  Σ2mxd = 2d Σmx
 
'Σmx' is a quantity which is proportional to the sum of moments of weights of various particles about the center of gravity G. Since a body can be balanced about its center of gravity ,
2d Σmx = 0
and substituiting this value in eqn (i) , we have
I = Ig + Md2
 
We hope this clarifies your doubt.
Regards
Team
Topperlearning
Answered by | 23 Nov, 2010, 01:33: PM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Physics
obtain the expression for time period of simple pendulum performing shm.
Asked by rustampathan | 25 Feb, 2024, 06:39: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
explain how angular momentum can be expressed as the vector product of two vectors.how is it's direction determined discuss the cases of minimum and maximum angular momentum
Asked by gipaalsy | 08 Feb, 2024, 05:41: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
t
question image
Asked by rkdubey133 | 19 Jan, 2024, 10:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
rotational motion
question image
Asked by priyankaprajapti81 | 04 Nov, 2023, 10:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
please answer
question image
Asked by gdeadshot85 | 14 Jan, 2023, 09:58: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
three diSc each of mass m and radius r placed in contact with each otheer find moment of inertia
Asked by devanshchauhan325 | 23 Dec, 2022, 07:34: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
Prove that Torque acting due to a Force F in the x-y plane is Tau z=xfy-yfx.
Asked by koushtubhroy | 20 Dec, 2022, 07:36: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
one meter long string can bear maximum of 0.5 kg mass . a mass of 0.05 kg is tied to one end and rotated in a horizontal circle , calculate the maximum number of revolution so that string does not brakes
Asked by pushpakumari291279 | 20 Aug, 2022, 08:15: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
A Uniform Disc of diameter R/2 is put over another uniform disc of radius R of same thickness and Density. The peripheries of the two discs touch each other. The Centre of Mass of the system from centre of the big disc is? (I asked this question before but the answer was wrong. They took the Radius as R/2 while it is the Diameter)
Asked by adipadmakarri | 26 Sep, 2021, 06:08: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
A Uniform Disc of diameter R/2 is put over another uniform disc of radius R of same thickness and Density. The peripheries of the two discs touch each other. The Centre of Mass of the system from centre of the big disc is?
Asked by adipadmakarri | 25 Sep, 2021, 11:18: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×