Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

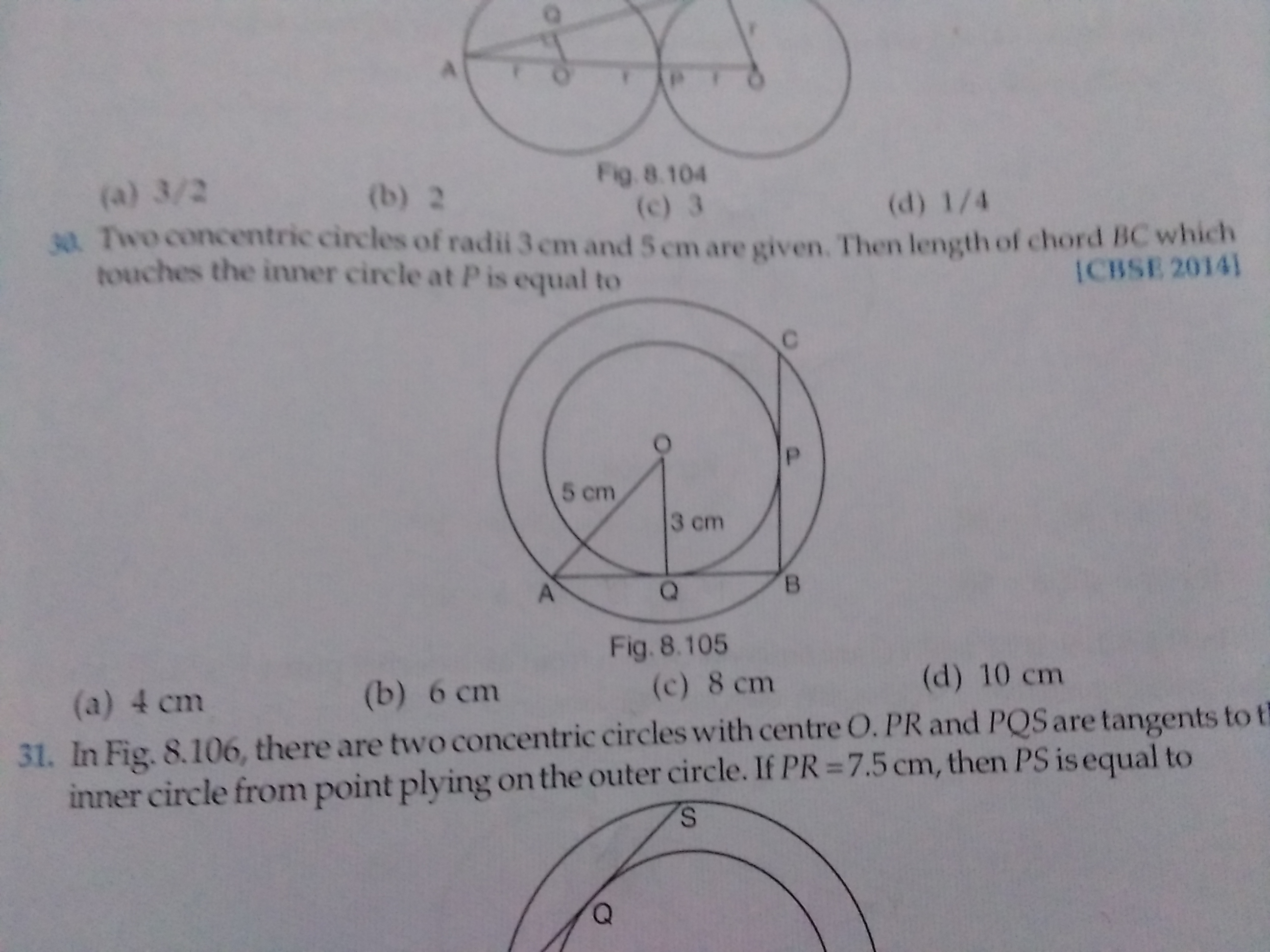
In fig., a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, B = 90o and DS = 5 cm, then the radius of the circle (in cm) is
Asked by nanda kumar | 22 Feb, 2014, 07:57: PM
answered-by-expert Expert Answer
Given that DS = 5 cm;
 
Since DS and DR are tangents from the same external point to the circle, DS = DR = 5 cm
 
Since AD = 23 cm, AR = AD - DR = 23 - 5 = 18 cm.
 
Similarly, AR and AQ are the tangents from the same external point to the circle and hence AR = AQ = 18 cm.
 
Since AB = 29 cm, BQ = AB - AQ = 29 - 18 = 11 cm.
 
Since CB and AB are the tangents to the circle, angle OPB and angle OQB is equal to 90 degrees.
 
Given that angle B is 90 degrees and hence angle POQ is also equal to 90 degrees and hence OQBP is a square.
 
Since BQ is 11 cm, the side of the square OQBP is 11 cm
 
From the figure it is clear that the side of the square is the radius of the circle and hence radius of the circle is 11 cm.
Answered by | 25 Feb, 2014, 09:24: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
PQ is a chord of length 8 cm to a circle of radius 5 cm. The tangents P and Q intersect at a point T. Find the length of the tangent TP.
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
in the given figure a triangle abc is drawn to circumscribe a circle of radius 3 cm such that the segment bd and dc are respectively of length 6 and 9 cm if the area of traingle abc is 54cm2 then find side ab and ac
question image
Asked by jennyy | 26 Mar, 2022, 08:41: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
3. Two supplementary angles are subtended at the centre by two arcs of a circle of radius 7 cm. Find the total length of these arcs  
Asked by sowmyashreeiyer | 31 Jan, 2022, 11:40: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
From a point P, two tangents PA and PB are drawn to a circle C(0, r).  If OP = 2r, then find ∠𝐴𝑃𝐵. What type of triangle is APB?  
Asked by riazu945 | 16 Jan, 2022, 01:00: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
in the above figure major
question image
Asked by ajabraosable27 | 11 Oct, 2021, 09:28: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
prime factorisation
Asked by amikasangma080 | 11 Oct, 2021, 06:14: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact
Asked by muskanmahek2411 | 08 Oct, 2021, 10:48: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
radious of circle is
Asked by anishasheoran372 | 13 Jul, 2021, 09:33: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
In the adjoining figure, AB is the Diameter of the circle. E is not the centre. Angle ACD = 30°. Find angle x.
question image
Asked by bhilarevishwesh | 21 May, 2021, 08:27: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Q30
question image
Asked by sangyaswarupa | 16 Mar, 2021, 10:06: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×