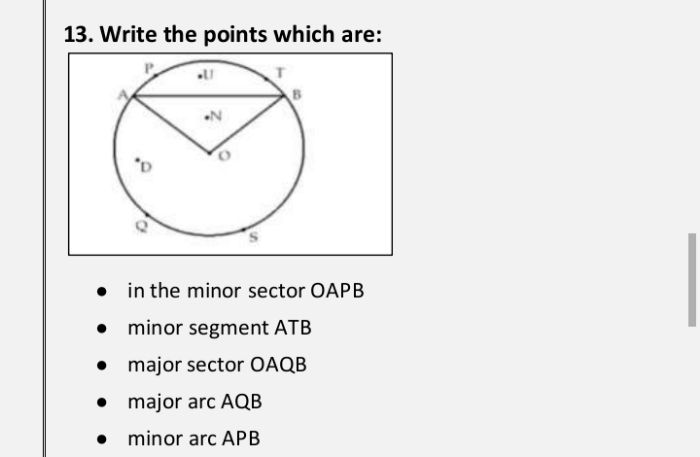
CBSE Class 9 Answered
In any triangle ABC,if the angle bisector of
Asked by anusarika mohanty | 22 Dec, 2013, 04:58: PM

Let perpendicular bisector of side BC and angle bisector of  A meet at point D.
A meet at point D.
Let perpendicular bisector of side BC intersects it at E.
Perpendicular bisector of side BC will pass through circum centre O of circle. Now, BOC and
BOC and  BAC are the angles subtended by arc BC at the centre and a point A on the remaining part of the circle respectively.
BAC are the angles subtended by arc BC at the centre and a point A on the remaining part of the circle respectively.
We also know that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
 BOC = 2
BOC = 2  BAC = 2
BAC = 2 A ... (1)
A ... (1)
In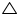 BOE and
BOE and 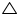 COE
COE
 A meet at point D.
A meet at point D.Let perpendicular bisector of side BC intersects it at E.
Perpendicular bisector of side BC will pass through circum centre O of circle. Now,
 BOC and
BOC and  BAC are the angles subtended by arc BC at the centre and a point A on the remaining part of the circle respectively.
BAC are the angles subtended by arc BC at the centre and a point A on the remaining part of the circle respectively. We also know that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
 BOC = 2
BOC = 2  BAC = 2
BAC = 2 A ... (1)
A ... (1) In
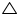 BOE and
BOE and 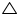 COE
COEOE = OE (common)
OB = OC (radii of same circle)
OB = OC (radii of same circle)
 OEB =
OEB =  OEC (Each 90o as OD
OEC (Each 90o as OD 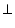 BC)
BC)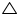 BOE
BOE 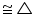 COE (RHS congruence rule)
COE (RHS congruence rule) BOE =
BOE =  COE (by CPCT) ... (2)
COE (by CPCT) ... (2) But
 BOE +
BOE +  COE =
COE =  BOC
BOC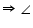 BOE +
BOE + BOE = 2
BOE = 2 A [Using equations (1) and (2)]
A [Using equations (1) and (2)]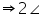 BOE = 2
BOE = 2 A
A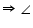 BOE =
BOE =  A
A BOE =
BOE =  COE =
COE =  A
AThe perpendicular bisector of side BC and angle bisector of  A meet at point D.
A meet at point D.
 A meet at point D.
A meet at point D. BOD =
BOD =  BOE =
BOE =  A ... (3)
A ... (3)Since AD is the bisector of angle  A
A
 A
A BAD =
BAD = 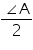
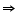 2
2 BAD =
BAD =  A ... (4)
A ... (4)From equations (3) and (4), we have
 BOD = 2
BOD = 2 BAD
BAD It is possible only if BD will be a chord of the circle. For this the point D lies on circum circle.
Therefore, the perpendicular bisector of side BC and angle bisector of
 A meet on the circum circle of triangle ABC.
A meet on the circum circle of triangle ABC.
Answered by | 22 Dec, 2013, 09:55: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by indu.suresh1220 | 27 Dec, 2023, 11:12: PM
CBSE 9 - Maths
Asked by subbusuchi1978 | 05 Nov, 2023, 10:24: AM
CBSE 9 - Maths
Asked by rameshsonkar1234ramesh | 21 Dec, 2022, 11:03: PM
CBSE 9 - Maths
Asked by sdmbotch1123 | 17 Dec, 2022, 09:39: PM
CBSE 9 - Maths
Asked by geetaradha8835 | 16 Dec, 2022, 07:59: PM
CBSE 9 - Maths
Asked by chalkekalyani80 | 06 Mar, 2022, 11:25: AM
CBSE 9 - Maths
Asked by sangeetabharti123456789 | 22 Feb, 2022, 09:01: AM
CBSE 9 - Maths
Asked by manognareddy.p28 | 25 Jul, 2021, 12:52: PM
CBSE 9 - Maths
Asked by Samidhaindulkar133 | 11 Mar, 2021, 04:03: PM