Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

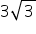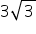In an equilateral triangle of side 3 square root of 3cm, find the length of the altitude.
Asked by Jerlin George | 21 Sep, 2015, 10:15: AM
answered-by-expert Expert Answer
 
 
 
begin mathsize 14px style Let space the space given space equilateral space triangle space be space ABC space Given colon space length space of space the space sides space equals space 3 √ 3 The space altitude space divides space the space equilateral space triangle space into space two space equal space right space angled space triangles. The space base space of space space triangle space ABC space gets space divided space into space two space equal space parts. Let space straight x space be space the space length space of space the space altitude. Consider space increment ABD Length space of space base space AD space equals 3 √ 3 divided by 2 space equals space fraction numerator space 3 √ 3 over denominator 2 end fraction space space The space sides space of space straight a space right space angled space triangle space ABD space satisfy space Pythagoras ’ space rule therefore open parentheses space 3 √ 3 close parentheses squared space equals space straight x squared space plus space open parentheses fraction numerator space 3 √ 3 over denominator 2 end fraction close parentheses squared therefore 27 space equals space straight x squared space plus space 27 over 4 therefore straight x squared space equals space 27 minus 27 over 4 therefore straight x squared space equals space fraction numerator 108 minus 27 over denominator 4 end fraction equals 81 over 4 therefore straight x equals square root of 81 over 4 end root equals 9 over 2 Therefore space length space of space altitude space equals space 4.5 space cm end style
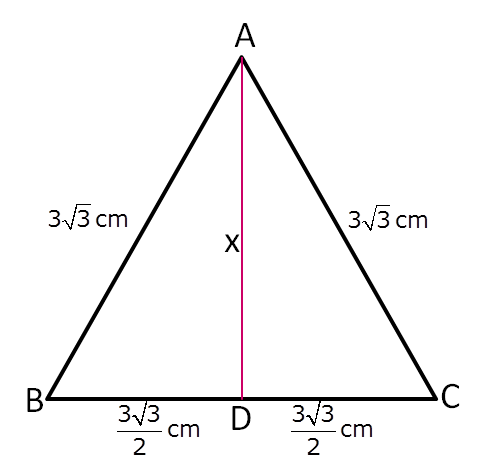
Answered by Priti Shah | 21 Sep, 2015, 09:12: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
ABCD is a rectangle in which diagonal AC is equals to 17 cm angle BCA is equals to thitha and sin theta is equals to 8/17 find the area of rectangle ABCDE (ii) the perimeter of rectangle ABCD
Asked by pathaksuman622 | 21 Apr, 2024, 11:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
the poles AB and CD of different heights are standing vertically on the ground level from a point P on the line joining the foots of the pole on the level of ground the angle of elevation to the top of the pole are founded to be complementary the of the CD and the distance PD 20√3m and 20m respectively if the BP is 10m then find the length of AB and the distance AC between the tpo of the poles
Asked by mraniruddha03 | 02 Apr, 2024, 06:44: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
√1+sin A/√1-sin A
Asked by vn3950372 | 18 Mar, 2024, 08:38: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
from the top of your vertical building of 350 m height on a level ground the angle of depression on of an object on the same ground is observed to be 60 degree find the distance of the object from the foot of the building
Asked by jayashreelatha04 | 17 Mar, 2024, 05:38: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
trigonometry
question image
Asked by vk952384 | 09 Mar, 2024, 11:34: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
find the value of cos20 if 2sin20 is root 3
Asked by gauravgupta.20008 | 03 Feb, 2024, 05:36: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
6. A is an acute angle in right triangle, right angled at B then value of (sinA + CosA) is ( a) Greater than (b) less than 1 (c) equal to 1 (d) depends on value of A
Asked by sathwicksathwick06 | 01 Feb, 2024, 07:30: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
solution
question image
Asked by pankajmali55 | 25 Jan, 2024, 07:51: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Q1. Ina DABC, LB=90^{\circ} If AB=2cm and AC=3cm Find Sin A.
Asked by tanujmaan58 | 18 Jan, 2024, 08:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
prove thar tan a-sin a/tan a+Sina, = sec a-1/sec A+1
Asked by balu162 | 16 Jan, 2024, 07:10: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×