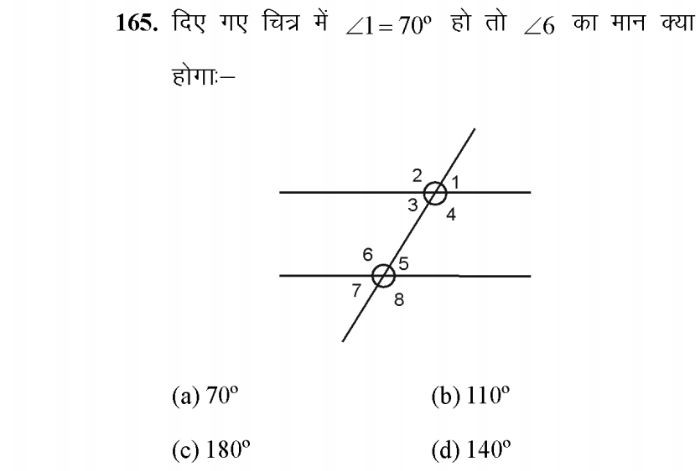
CBSE Class 9 Answered

the area of thetriangle ABC gets divided into threeparts i.e.

 area of OAB,OBC and OCA.

let the lengths of the perpendiculars  to AB,BC and CA be x ,y,z resply.

so

1/2[(AB)(x)]+1/2[(BC)(y)]+1/2[(CA)(z)]=area of ABC

but AB=BC=CA as the triangle is equilateral.

let AB=BC=CA=p (say)

so

x+y+z=2(area of ABC)/p

since area of the triangle ABC is fixed for given p, the right hand side is a constant number.

 so the sum of the perpendiculars

x+y+z is also a constant.