CBSE Class 9 Answered
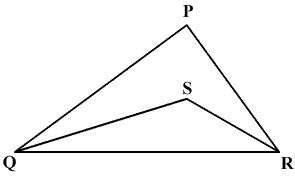
In a triangle, prove that the greater angle has the longer side opposite to it
Asked by gpnkumar0 | 05 Sep, 2016, 08:53: PM
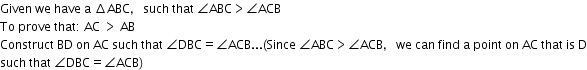 |
|
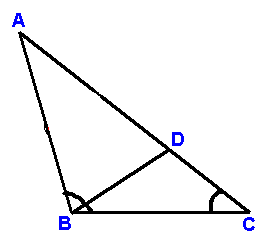  |
Answered by Rebecca Fernandes | 05 Sep, 2016, 10:53: PM
Concept Videos
CBSE 9 - Maths
Asked by kandalashyamala20 | 27 Dec, 2022, 02:30: PM
CBSE 9 - Maths
Asked by khardewsawrudolf | 22 May, 2020, 02:34: PM
CBSE 9 - Maths
Asked by vikasg13.hardware | 13 Jun, 2018, 12:01: PM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 08:45: AM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 08:47: AM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 08:47: AM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 10:06: AM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 10:04: AM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 08:40: AM