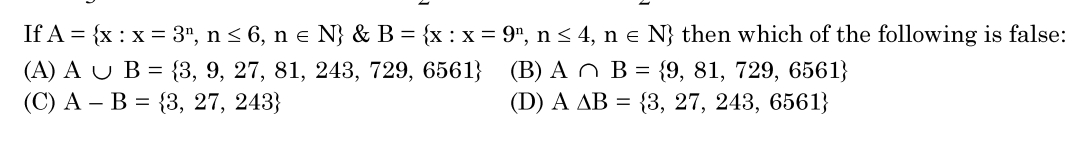CBSE Class 11-science Answered
In a town of 10,000 families, it was found that 40% families buy newspaper A, 20% families buy newspaper B and 10% families buy newspaper C. 5% families buy A and B, 3% families buy B and C and 4% buy A and C. If 2% families buy all three newspapers, find the number of families which buy (i) A only (ii) B only (iii) none A, B or C.
Asked by mesamit | 30 Jul, 2010, 10:26: AM
Expert Answer
Answered by | 30 Jul, 2010, 09:59: PM
Concept Videos
-
Types of sets and its representation
Types of sets and describe two forms of set representation. -
Subsets and Supersets
This video covers the definition of subsets and supersets of a set and also... -
Representing the union and intersection of sets
Venn diagrams. Represent the union and intersection of sets with the help o... -
Algebra of Sets
This video explains the concept of the difference of two given sets and rep... -
Counting Theorems ...
This video explains the application of set theory and Venn diagram to solve...
CBSE 11-science - Maths
Asked by parvanipatil09 | 29 Mar, 2024, 10:12: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by divyanshtikkiwal6 | 23 Feb, 2024, 07:44: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by pranavsrinivas82 | 14 Jan, 2024, 07:45: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by pranavsrinivas82 | 10 Jan, 2024, 08:45: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by naiduuofficial | 06 Jan, 2023, 07:49: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by anjaneyagadgil04 | 05 Jan, 2023, 12:16: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by bangtan7hybe | 18 Sep, 2022, 06:36: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by kdimple765 | 24 Jun, 2022, 04:22: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by arjunsah797 | 03 Mar, 2022, 06:04: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by krishkhare04 | 03 Feb, 2022, 02:35: PM
ANSWERED BY EXPERT
