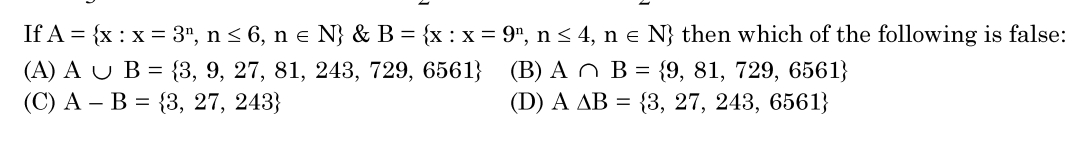Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

in a survey of 100 students, the number of students studying the various languages were found to be: english only 18, english but not hindi 23, englsih and sanskrit 8, english 26, sanskrit 48, sankrit and hindi 8, no launguage 24. find how many students were studying: (1) hindi (2) english and hindi (#) exactly one language (4)all 3 launguages (5)at least two of these languages (6) exactly 2 languages.
Asked by PriyaAnk ShaRma | 27 Jun, 2013, 12:32: PM
answered-by-expert Expert Answer

Let E, H and S denote the set of students who are studying English, Hindi and Sanskrit respectively.

Then, n (?) = 100

n (E) = 26

n (S) = 48

n (E ? S) = 8

n (S ? H) = 8

From the Venn-Diagram, it is clear that- n (E ? H ? S) = 3

The number of students who study English only = 18

Number of students who study no language = 24

? Number of students who study Hindi only = [100 – (18 + 5 + 3 + 5 + 35)] – 24

= 100 – 66 – 24

= 100 – 90

= 10

? Number of students who study Hindi

= 10 + 3 + 5

= 18

and Number of students who study English and Hindi = 3

3. Number of students who studies exactly one language = 18+35+10 = 63
 
4. All 3 languages n (E ? H ? S) = 3
 
5. at least 2 languages = n (E ? H) + n (E ? S) +n (H ? S) + n (E ? H ? S)
= 0+5+5+3 = 13
 
6. exactly 2 langauges = n (E ? H) + n (E ? S) +n (H ? S) 
= 0+5+5 = 10
 
So, yes the question is correct, except that here n (E ? H) = 0, which is not something that is always intutive from a venn diagram. 
 
If you have a worksheet of sets, please post 1 question/query on the website and we will solve all the questions for you. Please do not post multiple questions in the same query. 
Answered by | 27 Jun, 2013, 06:22: PM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Maths
in exercise 1.3 1st q ii part abc is not subset of bcd but two elements are common i.e bc but in 2 question same exercise i part ab is subset of  bca how ??  
Asked by parvanipatil09 | 29 Mar, 2024, 10:12: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Question no 21
question image
Asked by divyanshtikkiwal6 | 23 Feb, 2024, 07:44: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
how to represent Venn Diagram of A' and A.
Asked by pranavsrinivas82 | 14 Jan, 2024, 07:45: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
What is Venn Diagram
Asked by pranavsrinivas82 | 10 Jan, 2024, 08:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
the cardinal number of the set of letters of the word MATHEMATICS
Asked by naiduuofficial | 06 Jan, 2023, 07:49: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
If a set of the sets that are not member of itself is a member of itself
Asked by anjaneyagadgil04 | 05 Jan, 2023, 12:16: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
if u = [2,3,4.....,11] A=[2,4,7] B = [ 3,5,7,9,11] C =[7,8,9,10,11] COMPUTE 1] [A INTERSECTION U} intersection {BUC} 2] C - B  3] B - C 4] { B - C }'
Asked by bangtan7hybe | 18 Sep, 2022, 06:36: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
I am confused in a question from SETS AND RELATIONS P(A:B)={X:X∈P(A),B⊂X} In the given statement, does P(A:B) mean power set of ratio of set A and B? Please correct me if I am going wrong because I am not sure about it.
Asked by kdimple765 | 24 Jun, 2022, 04:22: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Does the set S={0,1,-1} form a group under multiplication?
Asked by arjunsah797 | 03 Mar, 2022, 06:04: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
PLEASE ANSWER THIS QUESTION ON SETS! 👇
question image
Asked by krishkhare04 | 03 Feb, 2022, 02:35: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×