CBSE Class 9 Answered
In a quadrilateral ABCD it is being given that M is the midpoint of AC.Prove that ar(ABMD)=ar(DMBC)
Asked by suprakash | 23 Dec, 2015, 10:41: PM
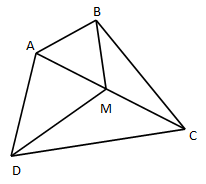

Answered by Rashmi Khot | 24 Dec, 2015, 10:16: AM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by bascaljoseph | 07 Feb, 2023, 01:27: PM
CBSE 9 - Maths
Asked by yadavPriy000 | 06 May, 2021, 07:11: PM
CBSE 9 - Maths
Asked by manugaur698 | 11 Sep, 2020, 04:30: PM
CBSE 9 - Maths
Asked by deepakumaraiya200 | 30 Jun, 2020, 09:51: AM
CBSE 9 - Maths
Asked by maddinenianr | 21 Mar, 2020, 03:48: PM
CBSE 9 - Maths
Asked by abhishema7 | 19 Jan, 2020, 12:29: PM
CBSE 9 - Maths
Asked by prakash.sanyasi | 04 Jan, 2020, 05:09: PM
CBSE 9 - Maths
Asked by kishor.kp14 | 15 Dec, 2019, 05:00: PM
CBSE 9 - Maths
Asked by ravinderchoudhary0486 | 06 Dec, 2019, 10:59: AM
CBSE 9 - Maths
Asked by suresh | 27 Nov, 2019, 09:21: PM











