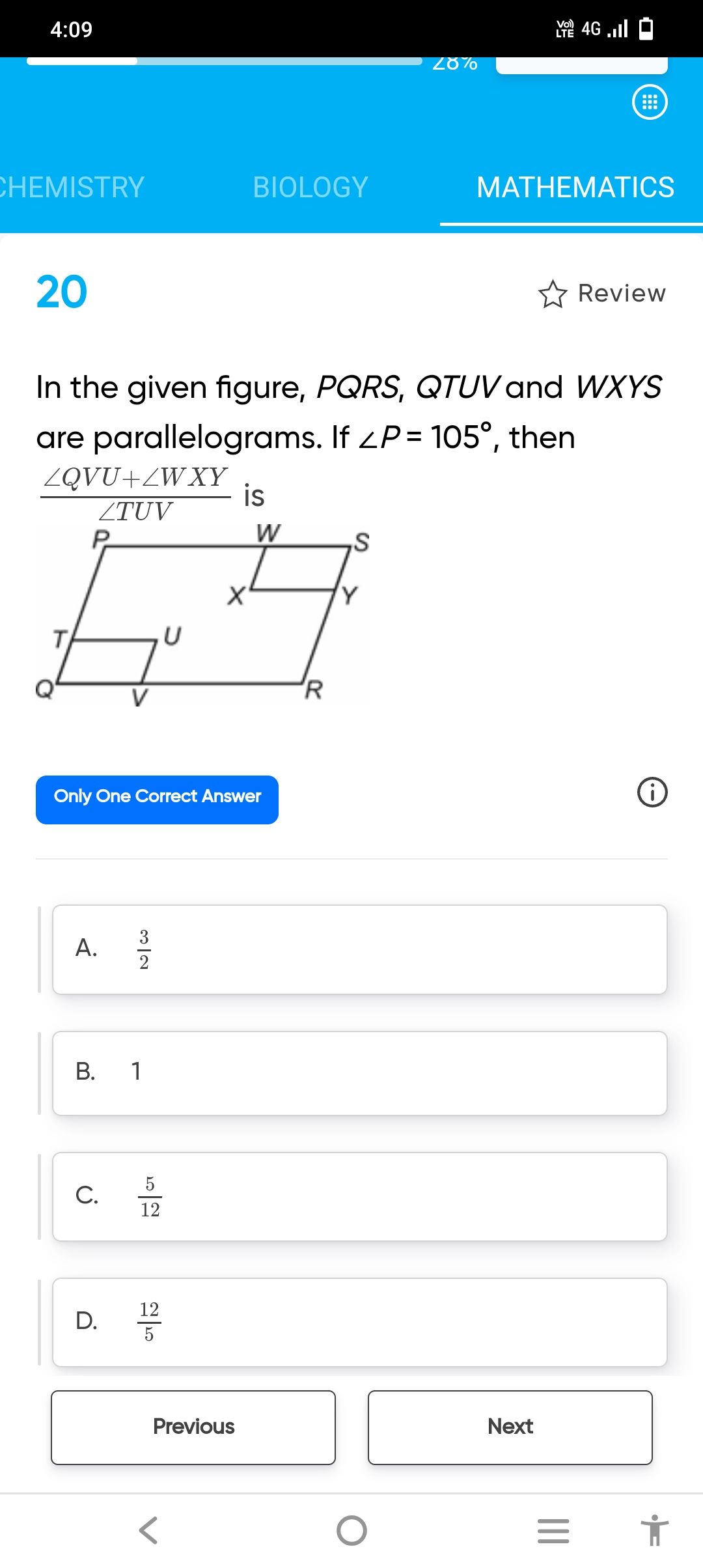
CBSE Class 9 Answered
In a parallelogram ABCD, E and F are the points on AB and CD such that AE=CE. Prove that ED is parallel to BF
Asked by | 17 Nov, 2013, 07:37: PM
Expert Answer
Given: ABCD is a parallelogram and AE = CF ...(1)
To Prove: ED
BF
Proof:
Since the opposite sides of the parallelogram are equal.
AB = CD ... (2)
Subtract (1) from (2):
AB - AE = CD - CF
BE = DF ... (3)
Also, BE is parallel to DF, therefore BEDF is a parallelogram.
Thus ED is parallel to BF.
Answered by | 17 Nov, 2013, 09:41: PM
Application Videos
-
Relation between Parallelogram and Triangle ...
This video explains the relation between the parallelogram and the triangle... -
Properties of a Parallelogram
This video contains a question which is solved using the property of a para... -
Use of Mid-point theorem
The video explains case study based type of question which is based on t...
-
Properties of Parallelogram
The video explains case study based type of question which is based on t...
-
Properties of quadrilateral
The video explains case study based type of question which is based on t...
Concept Videos
-
About relation between opposite angles in a parallelogr ...
Relation between opposite angles in a parallelogram. Explore the conditions... -
Relation between the diagonals of a parallelogram ...
Establish the relation between the diagonals of the parallelogram. Conditio... -
Mid Point Theorem
This video explains the Mid - Point theorem and its converse for a triangle... -
Types and Angle Sum Property
. Definition of Quadrilateral & special quadrilaterals: rectangle, square,... -
Parallelograms: Basic Properties
Parallelograms:Basic Properties
CBSE 9 - Maths
Asked by chandininayak86 | 15 Dec, 2023, 07:36: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by sagrawal0081 | 31 Aug, 2023, 07:24: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by jahnavinehra | 03 Jul, 2022, 11:19: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by seemarana8535 | 11 May, 2022, 04:17: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by abhiroy1462 | 16 Apr, 2022, 02:25: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by abdullahzedane2008 | 28 Mar, 2022, 12:11: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by sanskritiraghudev | 19 Feb, 2022, 09:38: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by varundhawan | 31 Jan, 2022, 10:41: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by aziznoorani17 | 04 Jan, 2022, 11:32: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by vineetyadav77050 | 25 Jul, 2021, 05:45: PM
ANSWERED BY EXPERT
