CBSE Class 9 Answered
In a parallelogram ABCD, E and F are the midpoints of sides AB and CD. Prove that the line segments AF and CE trisect the diagonal BD
Asked by Paresh | 11 Dec, 2015, 01:38: PM

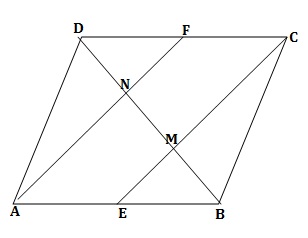

Answered by Vimala Ramamurthy | 11 Dec, 2015, 06:58: PM
Concept Videos
CBSE 9 - Maths
Asked by abhiroy1462 | 16 Apr, 2022, 02:25: PM
CBSE 9 - Maths
Asked by abdullahzedane2008 | 28 Mar, 2022, 12:11: PM
CBSE 9 - Maths
Asked by varundhawan | 31 Jan, 2022, 10:41: PM
CBSE 9 - Maths
Asked by riya.yanamandra | 19 Oct, 2020, 06:45: AM
CBSE 9 - Maths
Asked by shubhras445 | 27 May, 2020, 01:22: PM
CBSE 9 - Maths
Asked by vivaangolank | 10 Nov, 2019, 10:47: AM
CBSE 9 - Maths
Asked by Rajeshparve | 25 Oct, 2018, 10:40: PM
CBSE 9 - Maths
Asked by gspublicschool | 08 Sep, 2018, 06:04: AM
CBSE 9 - Maths
Asked by Topperlearning User | 17 Aug, 2017, 07:45: AM
CBSE 9 - Maths
Asked by Topperlearning User | 17 Aug, 2017, 07:45: AM




