Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

In a Hyperbola - The Triangle formed by an latus rectam with its farthest vertex is equilateral then find its ecentricity
Asked by Malavika Umesh | 01 May, 2015, 01:06: PM
answered-by-expert Expert Answer
Consider equation of a hyperbola in standad form.
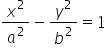
x squared over a squared minus y squared over b squared equals 1
Eccentricity 'e' is given by 
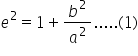
e squared equals 1 plus b squared over a squared..... left parenthesis 1 right parenthesis
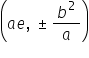
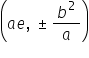
The coodinates of ends of latus rectum of one half of the hyperbola are open parentheses a e comma space plus-or-minus b squared over a close parentheses
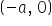
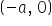
The coordinates of the vertex farther from the latus rectum are open parentheses negative a comma space 0 close parentheses
Since the triangle formed by these points is an equilateral triangle, equating the side lengths formed by these vertices we get
open parentheses a e plus a close parentheses squared plus open parentheses b squared over a close parentheses squared equals open parentheses fraction numerator 2 b squared over denominator a end fraction close parentheses squared rightwards double arrow open parentheses a e plus a close parentheses squared equals 3 open parentheses b squared over a close parentheses squared rightwards double arrow a e plus a equals square root of 3 open parentheses b squared over a close parentheses rightwards double arrow e plus 1 equals square root of 3 open parentheses b squared over a squared close parentheses
Adding square root of 3 to both sides of the above equation, we get 
e plus 1 plus square root of 3 equals square root of 3 open parentheses 1 plus b squared over a squared close parentheses.... left parenthesis 2 right parenthesis
From (1) and (2), we get 
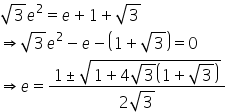
square root of 3 e squared equals e plus 1 plus square root of 3 rightwards double arrow square root of 3 e squared minus e minus open parentheses 1 plus square root of 3 close parentheses equals 0 rightwards double arrow e equals fraction numerator 1 plus-or-minus square root of 1 plus 4 square root of 3 open parentheses 1 plus square root of 3 close parentheses end root over denominator 2 square root of 3 end fraction
Taking only the posiive sign, as 'e' can not be negative, we get
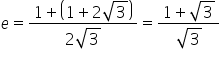
e equals fraction numerator 1 plus open parentheses 1 plus 2 square root of 3 close parentheses over denominator 2 square root of 3 end fraction equals fraction numerator 1 plus square root of 3 over denominator square root of 3 end fraction


Answered by satyajit samal | 03 May, 2015, 10:04: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Maths
2 one
question image
Asked by dra | 24 Feb, 2024, 06:35: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
find the coordinates of the centre of a circle passing through the points(0,0),(-2,1)and(-3,2).also , find its radius .
question image
Asked by shakyajayprakash2006 | 08 Jun, 2022, 05:26: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Examine whether the point (4, 5) lies outside or inside the circle of equation x^2+y^2-2x-3=0
Asked by sbipo2000 | 23 Feb, 2020, 03:43: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
SIR PLEASE HELP ME WITH THIS QUESTIONS : 1. Find the equation of the tangent to the circle x^2+y^2=16 drawn from the point (1,4). 2. How many triangles can be formed by joining any 3 of the 9 points when i) no 3 of them  are collinear? ii) 5 of them are collinear? 3. AB is a line of fixed length, 6 units, joining the points A(t,0) and B which lies on thepositive y axis. P is a point on AB distant 2 units from A. Express the coordinates of B and P in terms of t. Find the locus of P as t varies. 4. In a triangle ABC, (b^2 - c^2) / (b^2 + c^2) = sin(B - C) / sin(B + C), prove that it is either a right-angled or isoceles triangle.
Asked by kandappan | 08 Feb, 2020, 11:29: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
6
question image
Asked by gauravmore604 | 04 Nov, 2019, 03:31: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
The locus of point for which sum of the squares of distances from cordinate axes is 25 is
Asked by Tejravi969 | 19 Aug, 2019, 06:08: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
A stadium is in circular shape. Within the stadium some areas have been allotted for a hockey court and a javelin range, as given in the figure. Assume the shape of the hockey court and the javelin range to be square and triangle, resp. The curators would like to accommodate a few more sports in the stadium. Help them by measuring the unallocated region within the stadium.(the radius of the stadium is 200 mts.)  
Asked by rushabh1234 | 23 Jan, 2019, 08:59: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the equation of the circle with centre (-2,3) and radius 4.
Asked by Topperlearning User | 30 Apr, 2014, 11:08: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the centre and radius of the circle given by the equation (x + 5)2 + (y + 1 )2 = 9
Asked by Topperlearning User | 25 Apr, 2014, 09:39: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the co-ordinates of the centre and the radius of the circle given by the equation x2 + y2 + 6x - 8y - 24 = 0.
Asked by Topperlearning User | 25 Apr, 2014, 09:11: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×