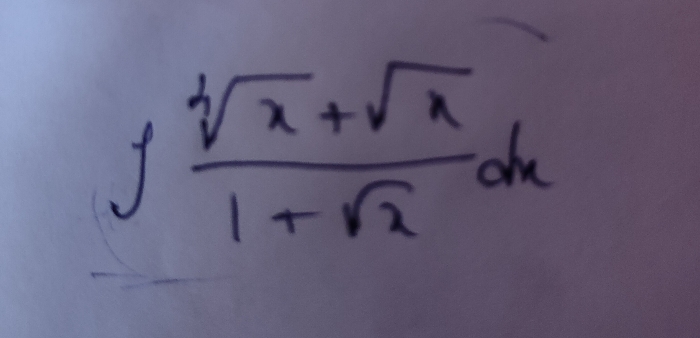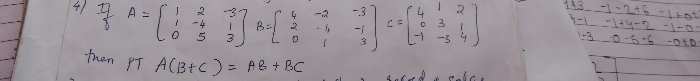CBSE Class 12-commerce Answered
In a city 1% of population is actually suffering from covid 19. A laboratory test is 95% effective is detecting the disease when it was actually present. however lab test yeilds a false positive results for 0.5% of healthy person's test. A person was selected for test and test report was positive, find the probality he was not loving disease.
Asked by mike010thedanger | 11 Dec, 2020, 11:22: AM
Let E1 and E2 be the events that a person suffering from COVID-19 and a person not not suffering from COVID-19.
As per the question P(E1) = 1/100 = 0.01
Now, P(E1) + P(E2) = 1
P(E2) = 1 - P(E1) = 1 - 0.01 = 0.99
P(A|E1) = 99% = 0.95
P(A|E2) = 0.5% = 0.005
Probability that a person not loving disease, given that his test result is positive, is given by P(E2∣A).
By using Baye's theorem, we obtain
P(E2|A) = P(E2) P(A|E2)/{P(E1) P(A|E1) + P(E2) P(A|E2)}By using Baye's theorem, we obtain
Answered by Renu Varma | 14 Dec, 2020, 02:00: PM
Application Videos
Concept Videos
CBSE 12-commerce - Maths
Asked by nainaadityathakur | 02 Apr, 2024, 12:56: PM
CBSE 12-commerce - Maths
Asked by nainaadityathakur | 17 Mar, 2024, 03:04: PM
CBSE 12-commerce - Maths
Asked by morninggood0966 | 29 Feb, 2024, 04:06: PM
CBSE 12-commerce - Maths
Asked by manishpaladiya652 | 28 Feb, 2024, 11:26: AM
CBSE 12-commerce - Maths
Asked by pathvipatel144 | 25 Feb, 2024, 09:37: PM
CBSE 12-commerce - Maths
Asked by nainaadityathakur | 06 Feb, 2024, 01:38: PM
CBSE 12-commerce - Maths
Asked by najakatkhan6698 | 25 Dec, 2023, 10:37: AM
CBSE 12-commerce - Maths
Asked by mounikachitrala342 | 26 Oct, 2023, 07:59: AM
CBSE 12-commerce - Maths
Asked by darshanasharma0409 | 21 Sep, 2023, 06:07: PM
CBSE 12-commerce - Maths
Asked by routdebasmita900 | 13 Aug, 2023, 10:43: AM