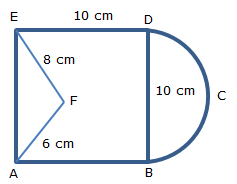
CBSE Class 10 Answered
in a circular table cover of radius 32 cm , a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. 12.24 . Find the area of the design.

Asked by azamk4198 | 14 Jan, 2016, 08:59: AM
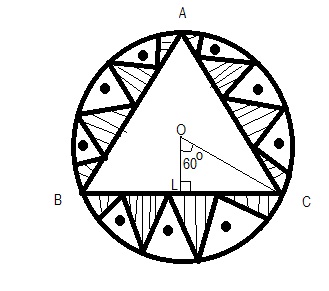
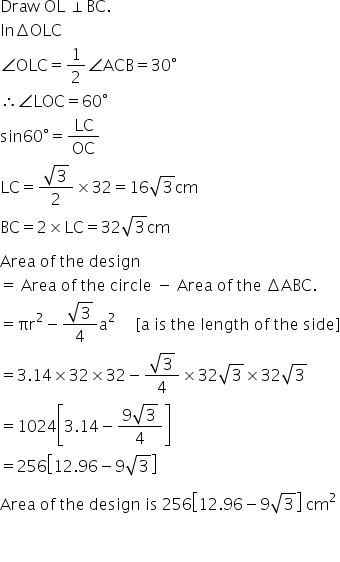
Answered by Vijaykumar Wani | 14 Jan, 2016, 12:05: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by Vidushi412 | 11 Aug, 2020, 10:20: PM
CBSE 10 - Maths
Asked by ssai6651 | 08 Jan, 2020, 07:39: AM
CBSE 10 - Maths
Asked by tejutanu2004 | 16 Sep, 2019, 08:27: PM
CBSE 10 - Maths
Asked by shailesh.solanki | 18 Mar, 2018, 07:29: PM
CBSE 10 - Maths
Asked by Topperlearning User | 27 Jul, 2017, 02:33: PM
CBSE 10 - Maths
Asked by Topperlearning User | 27 Jul, 2017, 02:33: PM
CBSE 10 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 10 - Maths
Asked by Topperlearning User | 27 Jul, 2017, 02:33: PM
CBSE 10 - Maths
Asked by Topperlearning User | 27 Jul, 2017, 02:28: PM
CBSE 10 - Maths
Asked by Topperlearning User | 27 Jul, 2017, 02:33: PM








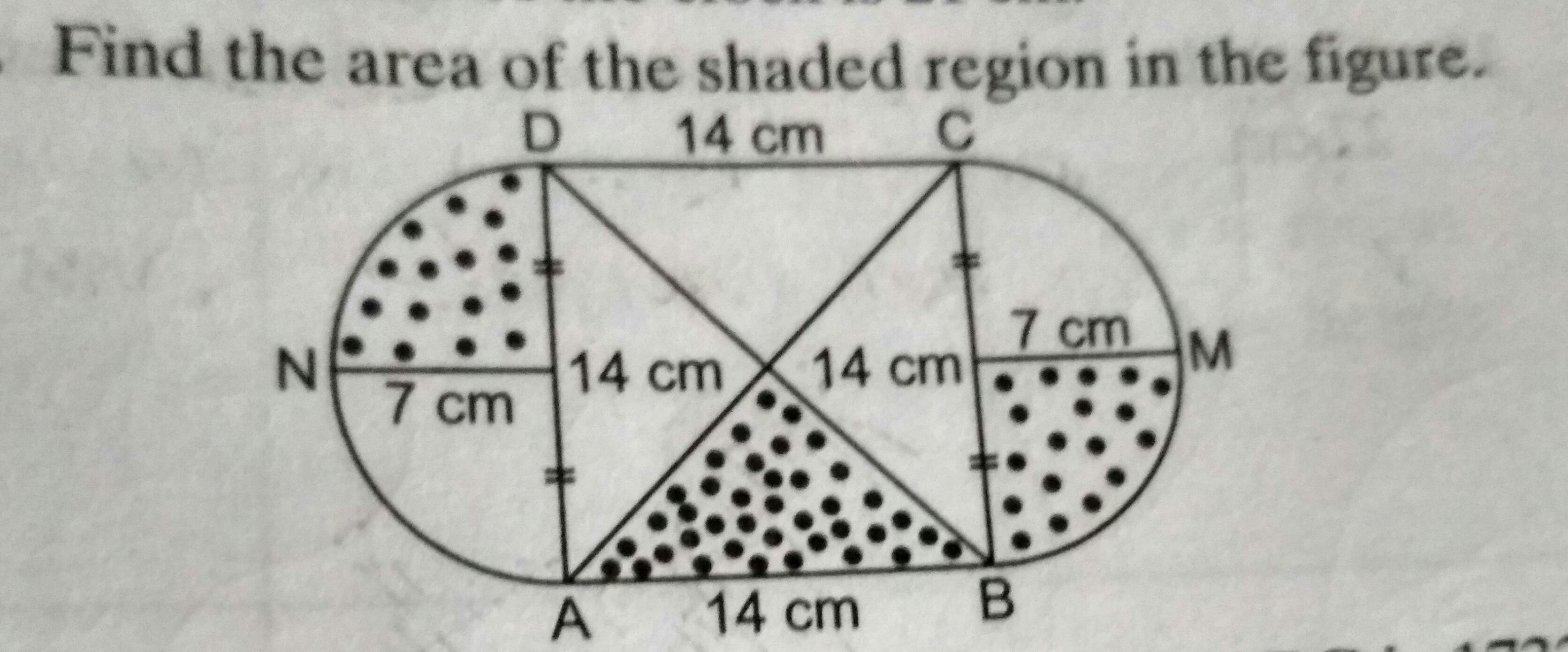
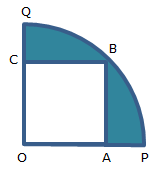

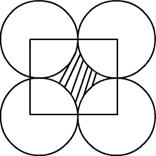
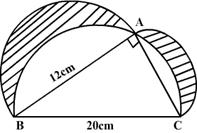
.jpg)