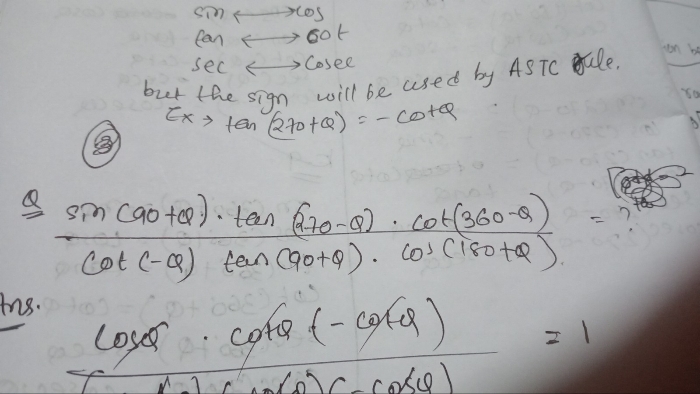CBSE Class 11-science Answered

Let A, B and C be three vertices of a triangle ABC. It is known that a unique circle can be drawn through any three points. Let O be the centre of such circle. Extend AO to a point D on the circle as shown below. Join CD. Let R be the radius of the circum-circle of triangle ABC i.e. OA = OD = R.

ACD is a triangle in a semicircle and therefore angle ACD = 90 degree.

In right angled ACD,

sin D = AC/AD

i.e. sin D = AC/2R                                                        … (1)

As angle B = angle D (because they stand on same arc AC), (1) above may be written

sin B = AC/2R

so 2R = AC/sin B

i.e. 2R = b/sin B                                                           … (2)

In a similar way, (drawing diameter from C etc) it can be shown that

2R = BC/sin A

i.e. 2R = a/sin A                                                          … (3)

and

2R = AB/sin C

i.e. 2R = c/sin C                                                           … (4)

From (2), (3) and (4);

a/sin A = b/sin B = c/sin C = 2R

Hence, proved