Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

Let space R space be space a space relation space f rom space N space t o space N space and space m space b e space a space given space fixed space p ositive space integer space such space that R space equals open curly brackets space left parenthesis space a comma b right parenthesis space : space a comma b space element of space Z space a n d space a minus b space i s space d i v s i b l e space b y space m space open space close curly brackets close. S h o w space t h a t space R space e q u i v a l e n c e space r e l a t i o n space
Asked by inderjeet.saluja | 27 Aug, 2014, 12:27: AM
answered-by-expert Expert Answer
The Relation R is an equivalence relation if and only if it satisfies the properties, Reflexivity, Symmetry and Transitivity.
 
Reflexivity: a is related to a because a-a is zero and zero divisible by any number and hence R is reflexive.
 
Symmetry: Assume that a is related to b, and hence a-b is divisible by m
 
Since a and b are integers, we have, a minus b equals m k subscript 1 space a n d space b minus a equals m k subscript 2 comma space w h e r e space k subscript 1 space a n d space k subscript 2 space a r e space a n y space i n t e g e r s and hence both are divisible by m.
Thus, R is Symmetric.
 
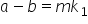
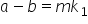
Transitivity: Iif a is related to b, we have, a minus b equals m k subscript 1
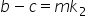
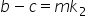
If b is related to c, we have, b minus c equals m k subscript 2
Now consider,
 a minus c equals a minus b plus b minus c equals m k subscript 1 plus m k subscript 2 equals m open parentheses k subscript 1 plus k subscript 2 close parentheses
Thus, a - c is divisible by m and hence a is related to c.
Thus, R is transitive.
Hence R is an equivalence relation.
Answered by Vimala Ramamurthy | 27 Aug, 2014, 08:59: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Maths
<div>.<img src="https://images.topperlearning.com/topper/tinymce/imagemanager/files/251b9929e126556d6b1e18c4cea63816570e7ef5923d58.16930475IMG20160413WA0017.jpg" alt="" /></div>
Asked by yugibo | 13 Apr, 2016, 10:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
<div> <div><img class="Wirisformula" src="https://images.topperlearning.com/topper/tinymce/integration/showimage.php?formula=706b7ed637e704fd1c14012a8d05cdad.png" border="0" alt="Let space R space be space a space relation space f rom space N space t o space N space and space m space b e space a space given space fixed space p ositive space integer space such space that R space equals open curly brackets space left parenthesis space a comma b right parenthesis space : space a comma b space element of space Z space a n d space a minus b space i s space d i v s i b l e space b y space m space open space close curly brackets close. S h o w space t h a t space R space e q u i v a l e n c e space r e l a t i o n space" align="middle" data-mathml="«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»Let«/mi»«mo»§#160;«/mo»«mi»R«/mi»«mo»§#160;«/mo»«mi»be«/mi»«mo»§#160;«/mo»«mi»a«/mi»«mo»§#160;«/mo»«mo»relation«/mo»«mo»§#160;«/mo»«mi»f«/mi»«mi»rom«/mi»«mo»§#160;«/mo»«mi»N«/mi»«mo»§#160;«/mo»«mi»t«/mi»«mi»o«/mi»«mo»§#160;«/mo»«mi»N«/mi»«mo»§#160;«/mo»«mi»and«/mi»«mo»§#160;«/mo»«mi»m«/mi»«mo»§#160;«/mo»«mi»b«/mi»«mi»e«/mi»«mo»§#160;«/mo»«mo»a«/mo»«mo»§#160;«/mo»«mi»given«/mi»«mo»§#160;«/mo»«mi»fixed«/mi»«mo»§#160;«/mo»«mi»p«/mi»«mi»ositive«/mi»«mo»§#160;«/mo»«mi»integer«/mi»«mspace linebreak=¨newline¨/»«mo»§#160;«/mo»«mi»such«/mi»«mo»§#160;«/mo»«mi»that«/mi»«mspace linebreak=¨newline¨/»«mi»R«/mi»«mo»§#160;«/mo»«mo»=«/mo»«mfenced open=¨{¨ close=¨¨»«mrow»«mo»§#160;«/mo»«mo»(«/mo»«mo»§#160;«/mo»«mi»a«/mi»«mo»,«/mo»«mi»b«/mi»«mo»)«/mo»«mo»§#160;«/mo»«mo»:«/mo»«mo»§#160;«/mo»«mi»a«/mi»«mo»,«/mo»«mi»b«/mi»«mo»§#160;«/mo»«mo»§#8712;«/mo»«mo»§#160;«/mo»«mi»Z«/mi»«mo»§#160;«/mo»«mi»a«/mi»«mi»n«/mi»«mi»d«/mi»«mo»§#160;«/mo»«mi»a«/mi»«mo»-«/mo»«mi»b«/mi»«mo»§#160;«/mo»«mi»i«/mi»«mi»s«/mi»«mo»§#160;«/mo»«mi»d«/mi»«mi»i«/mi»«mi»v«/mi»«mi»s«/mi»«mi»i«/mi»«mi»b«/mi»«mi»l«/mi»«mi»e«/mi»«mo»§#160;«/mo»«mi»b«/mi»«mi»y«/mi»«mo»§#160;«/mo»«mi»m«/mi»«mo»§#160;«/mo»«mfenced open=¨¨ close=¨}¨»«mo»§#160;«/mo»«/mfenced»«/mrow»«/mfenced»«mo».«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi»S«/mi»«mi»h«/mi»«mi»o«/mi»«mi»w«/mi»«mo»§#160;«/mo»«mi»t«/mi»«mi»h«/mi»«mi»a«/mi»«mi»t«/mi»«mo»§#160;«/mo»«mi»R«/mi»«mo»§#160;«/mo»«mi»e«/mi»«mi»q«/mi»«mi»u«/mi»«mi»i«/mi»«mi»v«/mi»«mi»a«/mi»«mi»l«/mi»«mi»e«/mi»«mi»n«/mi»«mi»c«/mi»«mi»e«/mi»«mo»§#160;«/mo»«mi»r«/mi»«mi»e«/mi»«mi»l«/mi»«mi»a«/mi»«mi»t«/mi»«mi»i«/mi»«mi»o«/mi»«mi»n«/mi»«mo»§#160;«/mo»«/math»" /></div> </div>
Asked by inderjeet.saluja | 27 Aug, 2014, 12:27: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×