Asked by commonuc | 9th Dec, 2015, 08:41: PM
Expert Answer:
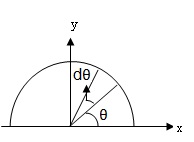
From the figure,
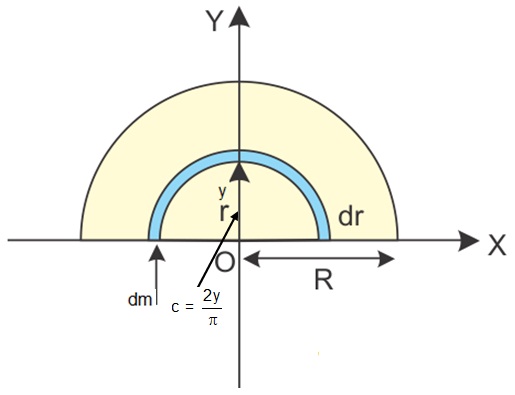
In case of disc, we consider ring element. Hence, half disc which is of width dy and radius y = r
Y coordinate of the disc can be treated as Y coordinate of it's centre of mass .
In the case of half disc centre of mass is located at the height, 
from the centre of ring.
In the case of half disc centre of mass is located at the height,
from the centre of ring.Answered by Priyanka Kumbhar | 10th Dec, 2015, 03:26: PM
Related Videos
- In which type of motion the position of centre of mass remains unchanged?
- What will be the position of centre of mass of a two particle system with unequal masses?
- What will be the position of centre of mass of a system having two particles of masses M and m (M > m) separated by a distance d?
- A projectile projected at a certain angle with the horizontal hits the ground at P. However, if this particle explodes at the highest point into two pieces of equal mass. One piece falls to the ground vertically downwards at Q, while the other travels horizontally and hit the ground at R. What is the distance of R from P?
- Explain briefly the motion of centre of mass?
- A body X of mass M while falling vertically downwards under the effect of gravity break in to two parts A and B having masses M/5 and 4M/5 respectively. How does the centre of mass of bodies A and B taken together shift compared to that of body X?
- There are two men standing facing each other on two boats floating on still water at a short distance apart. A rope is held at its ends by both. Explain why the two boats meet at same point when each man pulls the rope separately or both pull together? Will the time taken be different in the two cases? (Neglect Friction)
- Explain the motion of Earth-Moon system around the sun in terms of centre of mass concept.
- How will you prove that the centre of mass of two particles divides the line joining the particles in the inverse ratio of their masses?
- Two bodies of masses m1 and m2 are connected to the ends of a massless cord and allowed to move as shown. If the pulley is both massless and frictionless, find the acceleration of the centre of mass.
Kindly Sign up for a personalised experience
- Ask Study Doubts
- Sample Papers
- Past Year Papers
- Textbook Solutions
Sign Up
Verify mobile number
Enter the OTP sent to your number
Change