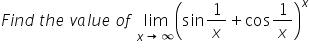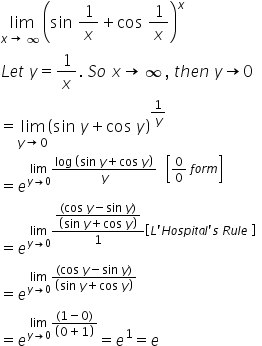CBSE Class 11-science Answered
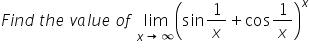
Asked by Topperlearning User | 10 Nov, 2016, 03:16: AM
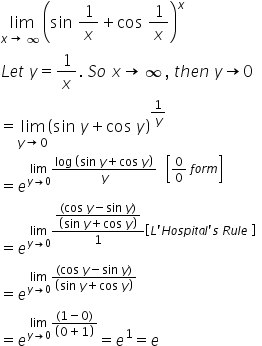
Answered by | 10 Nov, 2016, 05:16: AM
Join NOW to get access to exclusive study material for best results