Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

  if y = esinx + (tan x)x , prove that dy/dx = esin x cos x + (tan x)x [2x cosec 2x + log tan x]
Asked by haroonrashidgkp | 11 Jul, 2018, 12:18: PM
answered-by-expert Expert Answer
y = esinx + (tan x)x 
Let u =  esinx  and v = (tan x)x
u = esinx 
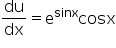begin mathsize 16px style du over dx equals straight e to the power of sinx cosx end style........(i)
 
v = (tanx)x 
log v = xlog tanx
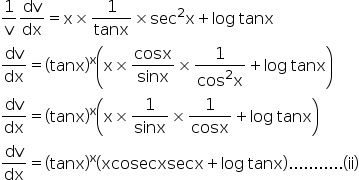
begin mathsize 16px style 1 over straight v dv over dx equals straight x cross times fraction numerator 1 over denominator tan begin display style straight x end style end fraction cross times sec squared straight x plus log space tanx space fraction numerator begin display style dv end style over denominator begin display style dx end style end fraction equals open parentheses tanx close parentheses to the power of straight x open parentheses straight x cross times fraction numerator cos begin display style straight x end style over denominator sin begin display style straight x end style end fraction cross times fraction numerator 1 over denominator begin display style cos squared end style begin display style straight x end style end fraction plus log space tanx close parentheses fraction numerator begin display style dv end style over denominator begin display style dx end style end fraction equals open parentheses tanx close parentheses to the power of straight x open parentheses straight x cross times fraction numerator 1 over denominator sin begin display style straight x end style end fraction cross times fraction numerator 1 over denominator begin display style cos straight x end style end fraction plus log space tanx close parentheses fraction numerator begin display style dv end style over denominator begin display style dx end style end fraction equals open parentheses tanx close parentheses to the power of straight x open parentheses xcosecxsecx plus log space tanx close parentheses........... left parenthesis ii right parenthesis end style
Error converting from MathML to accessible text.


Answered by Sneha shidid | 11 Jul, 2018, 02:26: PM

Concept Videos

Multiple Choice Questions Practice Test Subjective Questions Webinar Subjective Questions Pre Board Assessment
Answered Unanswered My Questions My Answers
CBSE 12-science - Maths
Find the derivative of log|-x|?
Asked by sdmbotch1123 | 21 Dec, 2022, 04:38: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
What is the maximum value of x^1/x
Asked by rk5488355 | 24 Jun, 2019, 09:48: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
                            ax............... if y = ax prove that dy/dx = y2(log y)/x{1 – y(logx)(logy)} explain in great detail  
Asked by haroonrashidgkp | 13 Aug, 2018, 08:40: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
  if y = esinx + (tan x)x , prove that dy/dx = esin x cos x + (tan x)x [2x cosec 2x + log tan x]
Asked by haroonrashidgkp | 11 Jul, 2018, 12:18: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
  If xmyn= (x+y)m+n, prove that dy/dx = y/x Mention each and every step
Asked by haroonrashidgkp | 19 Jun, 2018, 11:02: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
 If y = xcot x + 2x2 – 3/x2 + x + 2, find dy/dx Mention each and every step
Asked by haroonrashidgkp | 19 Jun, 2018, 10:57: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
 If y = (sin x)x + sin-1 (x)1/2, find dy/dx Mention each and every step
Asked by haroonrashidgkp | 19 Jun, 2018, 10:54: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
find dy/dx y = (log x)x + (x)log x mention each and every formula and minute details
Asked by haroonrashidgkp | 02 Jun, 2018, 08:30: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
find dy/dx  mention each and every formula and minute steps and detail Y = xx . e(2x + 5)
Asked by haroonrashidgkp | 02 Jun, 2018, 08:28: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Differentiate xsinx w. r. to x.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt

Be a Top Scorer in the Exam with Test Series and Test Generator!

Enrol Now
×