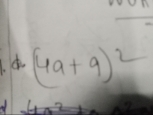ICSE Class 10 Answered
If x^p = y^q = (xy)^pq , show that p+q = 1
Asked by sinhayashvi90 | 23 Jun, 2022, 10:53: PM
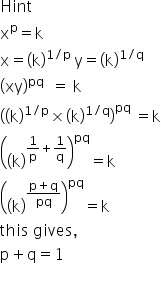
Answered by | 24 Jun, 2022, 01:37: AM
ICSE 10 - Maths
Asked by rameshmindi124 | 04 Dec, 2023, 01:27: PM
ICSE 10 - Maths
Asked by sinhayashvi90 | 23 Jun, 2022, 10:53: PM
ICSE 10 - Maths
Asked by p.sownthra2006 | 15 Jun, 2021, 05:36: PM