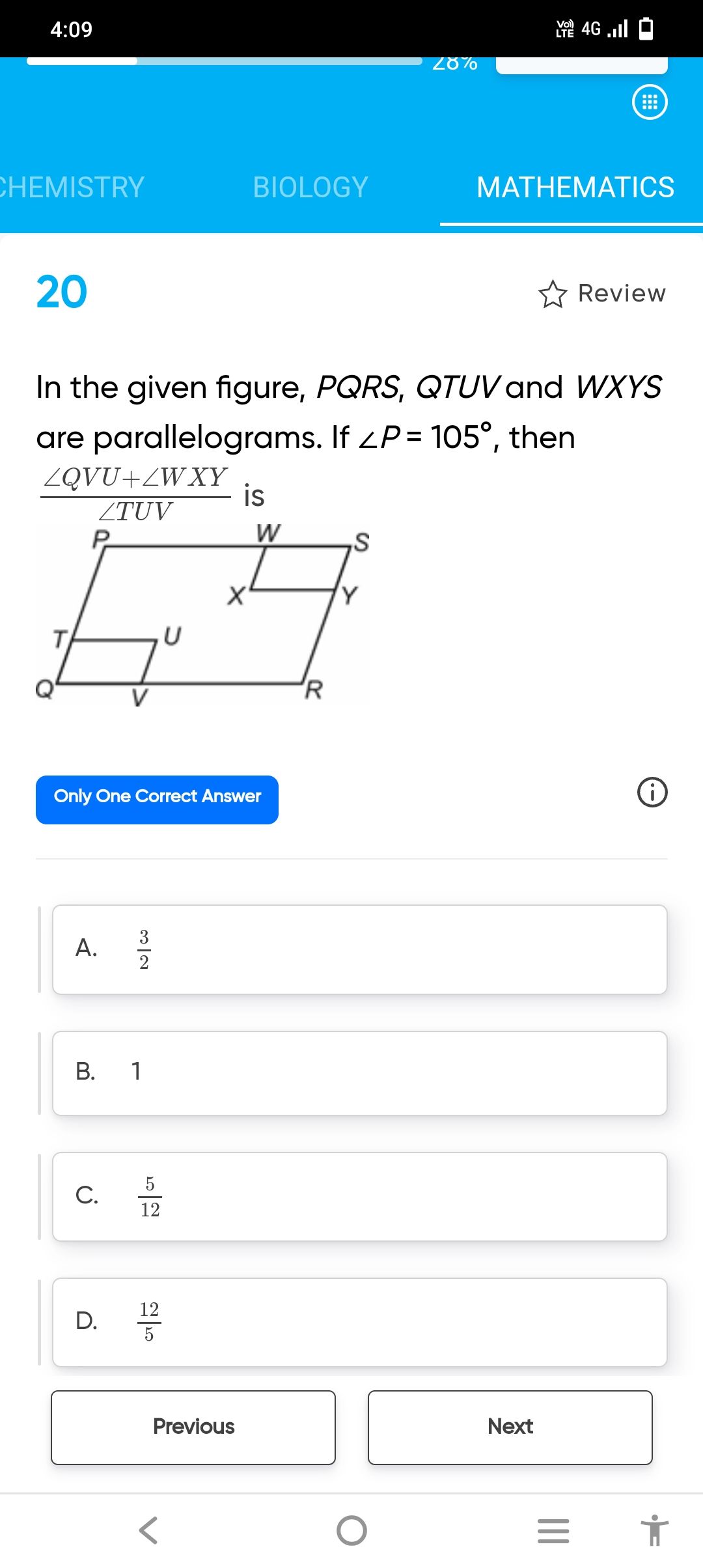
CBSE Class 9 Answered
if two opposite sides of a cyclic quadrilateral are parallel then prove that remaining two sides are equal and both the diagonals are equal
Asked by | 12 Mar, 2013, 10:41: PM
Expert Answer
Let ABCD be the cyclic quadrilateral with AD parallel to BC. The center of the circle is O.
Join AC
Now, since AD is parallel to BC and AC is the transverse
angle DAC = angle ACB (interior opposite angles)
angle DAC is subtended by chord DC on the circumference and angle ACB is subtended by chord AB.
If the angles subtended by 2 chords on the circumference of the circle are equal, then the lengths of the chords is also equal.
Hence, DC = AB i.e. the 2 remaining sides of the cyclic quadrilateral are equal.
Now, BD and AC are the 2 diagonals.
In triangle ABD and triangle DCA
AB = CD (proved above)
angle DCA = angle DAB (angles subtended by the same chord AD)
angle ACB = angle DAC(proved above)
Hence, triangle ABD is congruent to triangle DCA (by ASA)
hence, BD = AC (by CPCT)
Answered by | 13 Mar, 2013, 01:15: AM
Application Videos
-
Relation between Parallelogram and Triangle ...
This video explains the relation between the parallelogram and the triangle... -
Properties of a Parallelogram
This video contains a question which is solved using the property of a para... -
Use of Mid-point theorem
The video explains case study based type of question which is based on t...
-
Properties of Parallelogram
The video explains case study based type of question which is based on t...
-
Properties of quadrilateral
The video explains case study based type of question which is based on t...
Concept Videos
-
About relation between opposite angles in a parallelogr ...
Relation between opposite angles in a parallelogram. Explore the conditions... -
Relation between the diagonals of a parallelogram ...
Establish the relation between the diagonals of the parallelogram. Conditio... -
Mid Point Theorem
This video explains the Mid - Point theorem and its converse for a triangle... -
Types and Angle Sum Property
. Definition of Quadrilateral & special quadrilaterals: rectangle, square,... -
Parallelograms: Basic Properties
Parallelograms:Basic Properties
CBSE 9 - Maths
Asked by chandininayak86 | 15 Dec, 2023, 07:36: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by sagrawal0081 | 31 Aug, 2023, 07:24: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by jahnavinehra | 03 Jul, 2022, 11:19: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by seemarana8535 | 11 May, 2022, 04:17: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by abhiroy1462 | 16 Apr, 2022, 02:25: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by abdullahzedane2008 | 28 Mar, 2022, 12:11: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by sanskritiraghudev | 19 Feb, 2022, 09:38: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by varundhawan | 31 Jan, 2022, 10:41: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by aziznoorani17 | 04 Jan, 2022, 11:32: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by vineetyadav77050 | 25 Jul, 2021, 05:45: PM
ANSWERED BY EXPERT
