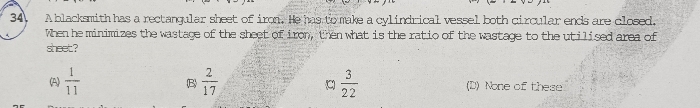CBSE Class 10 Answered
if the roots of the equation (b-c)xsquare+(c-a)x+(a-b)=0 are equal, then show that a,b,c are in AP.
Asked by riyaliz | 22 Jul, 2008, 10:17: PM
if the roots are equal , then discriminant b^2 - 4ac = 0
( c- a) ^2 - 4 ( b-c ) ( a-b) = 0
c^2 + a^2 - 2 ac - 4 [ ba-b^2 -ca +bc] = 0
c^ 2 + a^2 + 2ac + 4b^2 -4ab - 4bc = 0
[ c + a] ^2 = 4b [ a +c -b ]
if a, b,c are in A.P then c+a = 2b
substituting this c+a = 2b in the above equation , we will get [ c+a] ^2 = 4b[a+c -b] becomes
[ 2b ]^2 = 4b[ 2b - b] = 4b [ b] = 4b^2 THE CONDITION SATISFIES.
therefore a, b,c are in A.P
Answered by | 23 Jul, 2008, 06:24: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
CBSE 10 - Maths
Asked by rrajansinghakb199 | 08 Apr, 2024, 05:12: PM
CBSE 10 - Maths
Asked by nagalaxmidurgarao937 | 08 Apr, 2024, 01:42: PM
CBSE 10 - Maths
Asked by mraniruddha03 | 02 Apr, 2024, 06:44: PM
CBSE 10 - Maths
Asked by muttenenimalleswarrao | 29 Mar, 2024, 08:32: PM
CBSE 10 - Maths
Asked by pathakvaishnavi9139 | 23 Mar, 2024, 10:45: AM
CBSE 10 - Maths
Asked by mustafahssn786 | 23 Mar, 2024, 06:25: AM
CBSE 10 - Maths
Asked by choudharyniki001 | 22 Mar, 2024, 08:49: AM
CBSE 10 - Maths
Asked by jagdishdabang79 | 18 Mar, 2024, 08:40: PM