CBSE Class 10 Answered
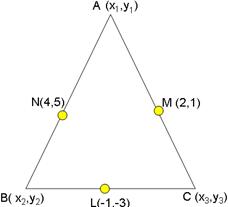
Let the vertices of the triangle be A(x1,y1), B(x2,y2) and C(x3,y3)
Let the given mid points of the sides BC, CA and AB be L(-1,-3), M(2,1) and N(4,5).
Now, by mid point formula,
-1 = ![]()
x2 + x3 = -2; x1 + x2 = 8; x1 + x3 = 4
2(x1 + x2 + x3) = 10
x1 + x2 + x3 = 5
On simplification,
x1 = 7, x2 = 1, x3 = -3
Similarly,
-3 =![]()
y2 + y3 = -6; y1 + y3 = 2; y1 + y2 = 10
2 (y1 + y2 + y3) = 6
y1 + y2 + y3 = 3
y1 = 9, y2 = 1, y3 = -7
Hence, the three vertices of the triangle are (7,9), (1,1) and (-3,-7).
OR
The given points are A(-2,5) , B(3,-4) and C(7,10).
AB = ![]()
BC = ![]()
CA = ![]() =
= ![]()
Since, AB = AC, ![]() ABC is an isosceles triangle.
ABC is an isosceles triangle.
Also, AB2 + AC2 = 106+ 106 =212 = BC2
Since, AB2+AC2
= BC2, ![]() ABC is also a right triangle.
ABC is also a right triangle.
Hence, ![]() ABC
is a right isosceles triangle.
ABC
is a right isosceles triangle.