Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

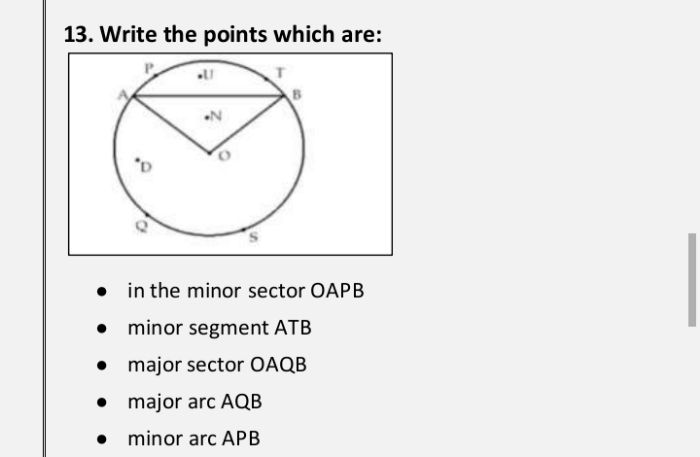
CBSE Class 9 Answered

If the circles are drawn taking two sides of a triangle as diameters ,prove that the point of intersection of these circles lie on the third side.
Asked by bansari Butani | 19 Feb, 2014, 02:14: PM
answered-by-expert Expert Answer
Dear Student,
 
Consider a triangleABC.
Two circles are drawn while taking AB and AC as the diameter.
Let they intersect each other at D and let D not lie on BC.
Join AD
 
∠ADB = 90°           (Angle subtended by semi-circle)
∠ADC = 90°            (Angle subtended by semi-circle)
∠BDC = ∠ADB + ∠ADC = 90° + 90° = 180°
 
Therefore, BDC is a straight line and hence, our assumption was wrong.
Thus, Point D lies on third side BC of ΔABC.
 
 
 
 
Thanks and Regards
Toppers Team
 
Answered by | 19 Feb, 2014, 06:19: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 9 - Maths
if the diameter AD of a circle is 34 cm and the length of a chord AB is 30 cm. what is the distance of AB from the ce
Asked by indu.suresh1220 | 27 Dec, 2023, 11:12: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
prove that of all chords of circle through a given point within it, the chord which is bisected at that point is the smallest
Asked by subbusuchi1978 | 05 Nov, 2023, 10:24: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
if two circles intersect at two points prove that their centres lie in the perpendicular bisector of the common chord
Asked by rameshsonkar1234ramesh | 21 Dec, 2022, 11:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
AB is chord of a circle with centre O. Let P and T be two points on the circumpherence such that < APB # < ATB and < APB = 80 degree then what is the value of < ATB.
question image
Asked by sdmbotch1123 | 17 Dec, 2022, 09:39: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
prove that the median bisecting the hypotenuse of a right angled triangle is half of the hypotenuse
Asked by geetaradha8835 | 16 Dec, 2022, 07:59: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
solution
question image
Asked by rairai4971 | 11 Jun, 2022, 09:03: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
three girls Reshma Salma And Mandeep are playing a game by standing on a circle of radius 5 drawn in a park Reshma throws a ball to Salma Salma To mandip mandip to Reshma if the distance between Reshma and Salman and between Salman Mandeep 6 each what is the distance between Reshma Mandip
Asked by chalkekalyani80 | 06 Mar, 2022, 11:25: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that equal chords of a circle subtend equal angles at the centre.
Asked by sangeetabharti123456789 | 22 Feb, 2022, 09:01: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
What is a tangent?
Asked by manognareddy.p28 | 25 Jul, 2021, 12:52: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that the angle at the centre of a circle is twice the angle at the remaining part of the circle.
Asked by Samidhaindulkar133 | 11 Mar, 2021, 04:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×