CBSE Class 11-science Answered
If tan B = 2sinA sinC/ sin (A+C) , show that cotA,cotBand cotC are in A.P .
Asked by Sanjay | 13 May, 2015, 12:20: AM
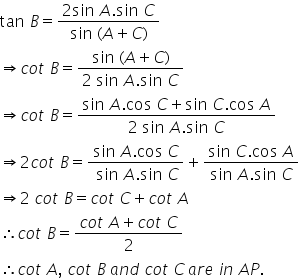
Answered by Prasenjit Paul | 13 May, 2015, 10:33: AM
Concept Videos
CBSE 11-science - Maths
Asked by rajyothi64 | 05 Mar, 2024, 09:49: PM
CBSE 11-science - Maths
Asked by ghoshshawata62 | 04 Mar, 2024, 08:16: PM
CBSE 11-science - Maths
Asked by nayaktapaswini2007 | 29 Feb, 2024, 09:10: AM
CBSE 11-science - Maths
Asked by bimanmandal53361 | 15 Jan, 2024, 12:32: AM
CBSE 11-science - Maths
Asked by sreyas.katuri | 23 Sep, 2023, 07:12: AM
CBSE 11-science - Maths
Asked by 069.pks | 16 Sep, 2023, 10:06: AM
CBSE 11-science - Maths
Asked by surekhashriwas01 | 12 Sep, 2023, 08:39: PM
CBSE 11-science - Maths
Asked by mvr23467 | 12 Sep, 2023, 07:52: PM
CBSE 11-science - Maths
Asked by SasipriyaNagappan | 27 Jul, 2023, 07:22: PM