Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

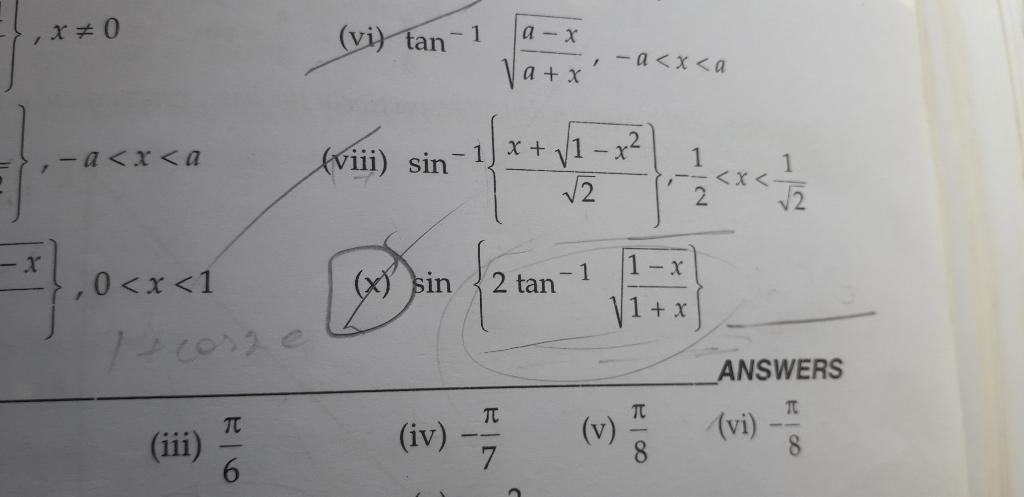
CBSE Class 12-science Answered

If sin^-1x+sin^-1y+sin^-1z=pi,prove that 
(i) x(1-x^2)^1/2 +y(1-y^2)^1/2 +z(1-z^2)^1/2=2xyz
(ii) x^4 +y^4 +z^4 +4x^2 y^2 z^2 =2(x^2 y^2 +y^2 z^2+z^2-- x^2
Asked by Balbir | 28 Apr, 2017, 09:19: PM
answered-by-expert Expert Answer
begin mathsize 16px style Let comma space sin to the power of negative 1 end exponent straight x equals straight A comma space sin to the power of negative 1 end exponent straight y equals straight B comma space sin to the power of negative 1 end exponent straight z equals straight C straight A plus straight B plus straight C equals straight pi Here space to space prove space that space sin space 2 straight A plus space sin 2 straight B plus sin 2 straight C equals 4 sinAsinBsinC LHS equals 2 sin left parenthesis straight A plus straight B right parenthesis cos left parenthesis straight A minus straight B right parenthesis plus 2 sinCcosC equals 2 sinCcos left parenthesis straight A minus straight B right parenthesis plus 2 sinCcosC equals 2 sinC left square bracket cos left parenthesis straight A minus straight B right parenthesis plus cosC right parenthesis right square bracket equals 2 sinC left square bracket cos left parenthesis straight A minus straight B right parenthesis minus cos left parenthesis straight A plus straight B right parenthesis right square bracket equals 2 sinC 2 sinBsinA equals 4 sinAsinBsinC straight x square root of 1 minus straight x squared end root plus straight y square root of 1 minus straight y squared end root plus straight z square root of 1 minus straight z squared end root equals 2 sinAsinBsinC equals 2 xyz end style
 
 
begin mathsize 16px style sin to the power of negative 1 end exponent straight x plus sin to the power of negative 1 end exponent straight y plus sin to the power of negative 1 end exponent straight z equals straight pi sin to the power of negative 1 end exponent straight x plus sin to the power of negative 1 end exponent straight y equals straight pi minus sin to the power of negative 1 end exponent straight z sin to the power of negative 1 end exponent open parentheses straight x square root of 1 minus straight y squared end root plus straight y square root of 1 minus straight x squared end root close parentheses equals open parentheses straight pi minus sin to the power of negative 1 end exponent straight z close parentheses open parentheses straight x square root of 1 minus straight y squared end root plus straight y square root of 1 minus straight x squared end root close parentheses equals sin open parentheses straight pi minus sin to the power of negative 1 end exponent straight z close parentheses straight x square root of 1 minus straight y squared end root plus straight y square root of 1 minus straight x squared end root equals straight z Taking space square space on space both space sides space and space simplifying comma straight x squared minus straight y squared minus straight z squared equals 2 yz square root of 1 minus straight x squared end root squaring space on space both space sides comma straight x to the power of 4 plus straight y to the power of 4 plus straight z to the power of 4 minus 2 straight x squared straight y squared plus 2 straight y squared straight z squared minus 2 straight z squared straight x squared equals 4 straight y squared straight z squared minus 4 straight x squared straight y squared straight z squared straight x to the power of 4 space plus straight y to the power of 4 space plus straight z to the power of 4 space plus 4 straight x squared space straight y squared space straight z squared space equals 2 left parenthesis straight x squared space straight y squared space plus straight y squared space straight z squared plus straight z squared space straight x squared right parenthesis end style
Answered by Sneha shidid | 02 May, 2017, 10:14: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Maths
solve it
question image
Asked by sdmbotch1123 | 19 Sep, 2023, 01:53: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Solve it pls.
question image
Asked by sdmbotch1123 | 10 Apr, 2023, 10:55: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Evaluate 3 sin -1 (1/root 2) + 2 cos -1 (root3/2) + cos-1(0)
Asked by varma.renu9481 | 13 Mar, 2023, 11:51: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Sin^-1x = cos^-1x, 0<x<1. Solve  
question image
Asked by w3ctiger | 12 Feb, 2023, 11:55: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
tan¹x + tan¹y=π+tan¹(x+y/1-xy), xy>1;x, y>0
Asked by joymaibam38 | 26 Dec, 2021, 09:04: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
peinciple branch od sec -¹ x
Asked by naikmanjuank | 17 Sep, 2020, 11:48: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
tan^-1x-1/x-2+tan^-1x+1/x+2=pi/4.find value of x.   
Asked by sshas3199 | 23 Aug, 2020, 09:24: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
  Consider the equation . Choose the CORRECT option(s). The sum of all solutions = 0< The number of solutions = 2< The number of solution = 1< The sum of squares of all solutions = 1<
Asked by harshsharma2531 | 09 Aug, 2020, 09:28: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Sin(sin-11/5+cos-1x)=1 Find value of x?
Asked by raiannu064 | 16 Jan, 2020, 01:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Plz solve (x) part Find the value of x
question image
Asked by lovemaan5500 | 04 Jan, 2020, 11:12: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×