CBSE Class 12-science Answered
If R and S are symmetric relations on the set A, then prove that 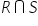 and
and 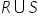 are symmetric.
are symmetric.
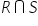 and
and 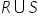 are symmetric.
are symmetric.
Asked by abhinavsaini123 | 01 Jun, 2015, 08:57: PM

Answered by Prasenjit Paul | 02 Jun, 2015, 10:50: AM
Application Videos
Concept Videos
CBSE 12-science - Maths
Asked by 20muskaansharma23 | 08 Apr, 2024, 11:31: AM
CBSE 12-science - Maths
Asked by nainaadityathakur | 12 Mar, 2024, 01:22: PM
CBSE 12-science - Maths
Asked by aiswaryaanil0009 | 01 Feb, 2024, 08:36: PM
CBSE 12-science - Maths
Asked by raunakumar9300 | 01 Feb, 2024, 04:23: PM
CBSE 12-science - Maths
Asked by amandwivesh | 25 Oct, 2023, 11:57: PM
CBSE 12-science - Maths
Asked by bornalimalakar3 | 05 Oct, 2023, 11:15: AM
CBSE 12-science - Maths
Asked by rginish12 | 04 Oct, 2023, 11:14: AM
CBSE 12-science - Maths
Asked by sdmbotch1123 | 19 Sep, 2023, 01:53: PM
CBSE 12-science - Maths
Asked by iamujjy | 21 May, 2023, 04:55: PM













