CBSE Class 11-science Answered
When a wire is put under a tensile stress,work is done against the inter-atomic forces.
This work is stored in the wire in the form of elastic potential energy.
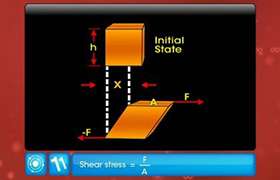
When a wire of original length L and area of cross-section A is subjected to a deforming force F along the length of the wire.
let the length of the wire is elongated by l.
now from Hookes law , we know that
Y = stress / strain.
Also here stress = Force(F)/area (A)
And strain = l/L
Hence Y = (F/A)/(l/L)
F= YA (l/L). Here Y is the Youngs modulus of the material of the wire. Now for a further
elongation of infinitesimal small length dl, then the work done:
dW is F * dl or
Y A ld l /L.
Therefore the amount of work done (W) in increasing the length of the wire from
l to L +l, that is from l = 0 to l = l is
= (YA/2) * l2/L
= ½ * Y *(l/L)2 *AL
= ½ * youngs modulus * strain2 * volume of the wire
= ½ * stress *strain *volume of the wire
This work is stored in the wire in the form of elastic potential energy (U). Therefore the
elastic potential energy per unit volume of the wire (U) is
U = ½ ? ?