CBSE Class 12-science Answered
If OT and ON are respectively the lengths of the perpendiculars drawn from the origin to the tangent and normal drawn at any arbitrary point on the curve, 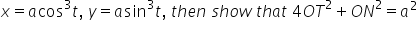 .
.
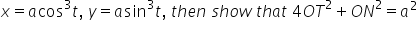 .
.
Asked by Aswin | 05 Jan, 2016, 05:43: PM

Answered by satyajit samal | 06 Jan, 2016, 05:52: PM
Concept Videos
CBSE 12-science - Maths
Asked by agarwalgolu318 | 13 Aug, 2020, 08:09: PM
CBSE 12-science - Maths
Asked by givduf | 11 Jul, 2020, 09:00: AM
CBSE 12-science - Maths
Asked by sonalchoudhary882 | 22 Oct, 2018, 12:22: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 08:27: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 08:32: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 09:19: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 09:58: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 10:14: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 11 Aug, 2014, 10:06: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 12:43: PM




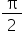 is
is