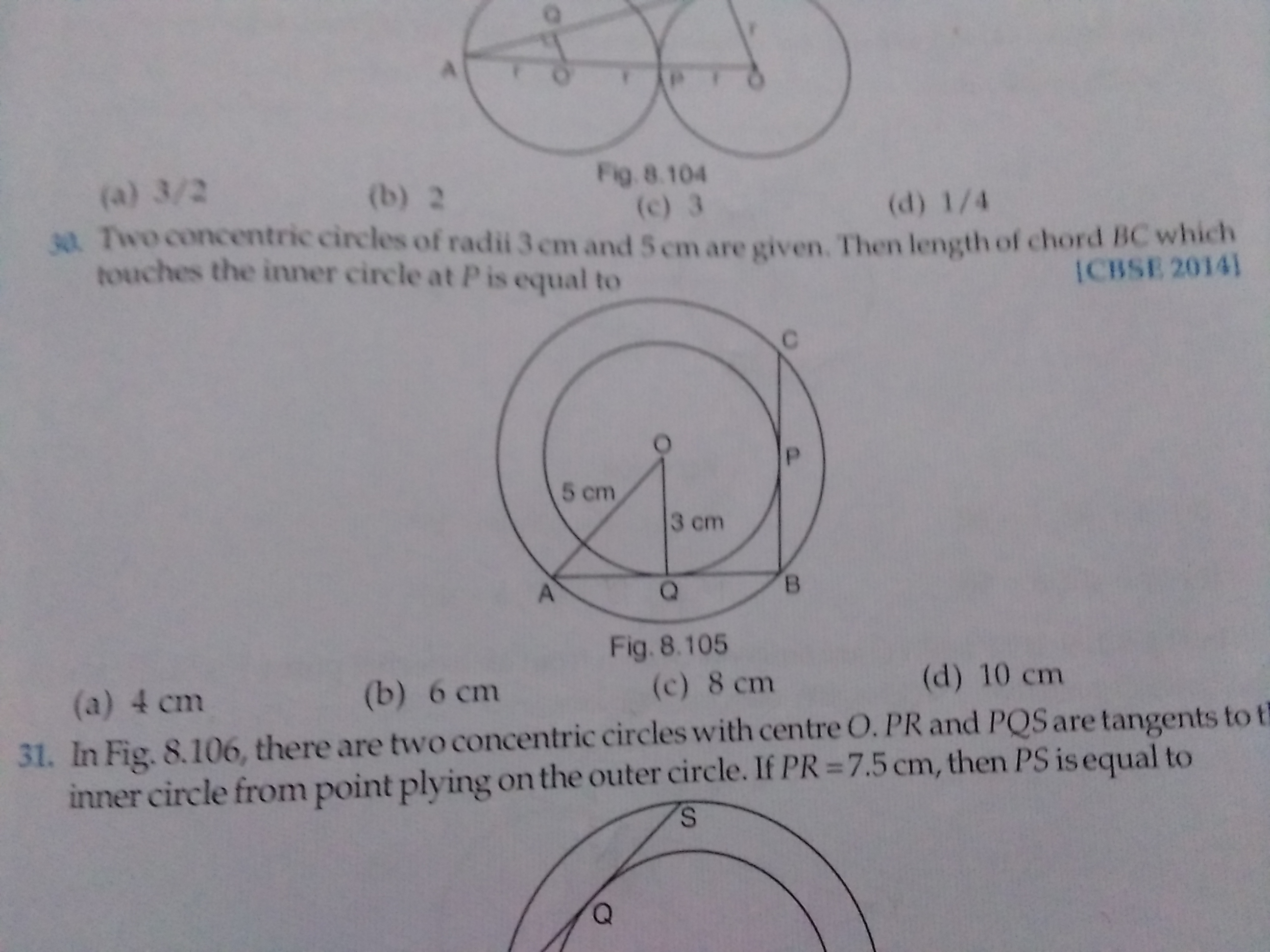
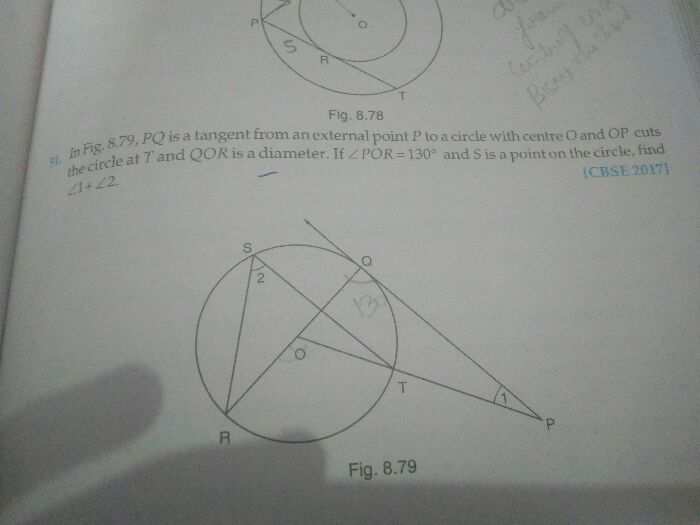
CBSE Class 10 Answered
If d1,d2 (d2>d1)
are the diameters of two concentric circles and c is
the length of a chord of a circle
which is tangent to the other circle,
then prove that d22=
c2+d12.
Asked by Topperlearning User | 27 Jul, 2017, 01:27: PM
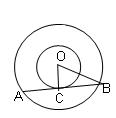
Let AB = c be a chord of the larger circle, of diameter d2, which
touches the other circle at C. Then ∆OCB is a right triangle.
By Pythagoras theorem,
OC2+BC2=OB2
i.e.
, ![]() (as C bisects AB)
(as C bisects AB)
Therefore, d22= c2+d12
Answered by | 27 Jul, 2017, 03:27: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
CBSE 10 - Maths
Asked by riazu945 | 16 Jan, 2022, 01:00: PM
CBSE 10 - Maths
Asked by sinhkaran79 | 14 Mar, 2021, 12:59: PM
CBSE 10 - Maths
Asked by s.saumya1011 | 05 Nov, 2020, 02:10: PM
CBSE 10 - Maths
Asked by brjkishorchauhan03 | 04 Nov, 2020, 12:10: PM
CBSE 10 - Maths
Asked by shivappahb308 | 21 Sep, 2020, 02:15: PM
CBSE 10 - Maths
Asked by VasupradUboveja376 | 22 Jun, 2020, 12:03: AM