Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 9 Answered

If AD is a median of triangle ABC and P is a point on AC such that ar(ADP): ar(ABD) = 2:3, then ar(PDC) : ar (ABC) is??
Asked by kumar.ashlesha | 12 Dec, 2014, 08:37: PM
answered-by-expert Expert Answer
fraction numerator A r. space A D P over denominator A r. space A B D end fraction equals 2 over 3 A r. space A D P space equals space 2 x comma space A r. space A B D space equals 3 x A r. space A B D space equals A r. space A D C space equals 3 x left square bracket S I n c e space A D space i s space t h e space m e d i a n space a n d space A D space d i v i d e s space t h e space t r i a n g l e space i n t o space t w o space t r i a n g l e s space o f space e q u a l space a r e a s right square bracket A r. space A D C space equals A r. space A D P plus A r. space P D C rightwards double arrow 3 x equals 2 x plus A r. space P D C rightwards double arrow A r. space P D C equals x A r. space A B C space equals space A r. space A B D plus A r. space A D C equals 3 x plus 3 x equals 6 x fraction numerator A r. P D C over denominator A r. space A B C end fraction equals fraction numerator x over denominator 6 x end fraction equals 1 over 6
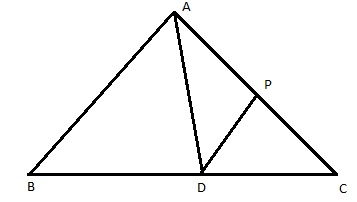
Answered by Prasenjit Paul | 13 Dec, 2014, 09:57: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 9 - Maths
area of right triangle is 240cm and side other than hypotenuse is 30cm.find the perimeter
Asked by bascaljoseph | 07 Feb, 2023, 01:27: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
find the percentage increase in the area of the triangle if it side is doubled
Asked by deepakumaraiya200 | 30 Jun, 2020, 09:51: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
an isosceles right angled triangle has an area of 8cm square.find the lenght of its hypotenuse.
Asked by kishor.kp14 | 15 Dec, 2019, 05:00: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
The sides of a triangular plot are in the ratio of 3:5:7 and it's perimeter is300 meter .find its area
Asked by ravinderchoudhary0486 | 06 Dec, 2019, 10:59: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
The sides of triangular park in ratio of 2:6:7 and it perimeter is 300m.  Then its area is   
Asked by kumarvsteel477 | 12 Sep, 2019, 08:22: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Find the area of an isosceles triangle whose perimeter is 60cm and each of equal sides is 24cm  
Asked by phukansayan5 | 28 Aug, 2019, 06:16: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
If the area of an equilateral triangle is 16√3cmsq then find the perimeter of the triangle 
Asked by arunpssac | 19 Aug, 2019, 07:02: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
the base of a triangular field is three times its altitude is the cost of sowing the field at rupees 58 per hectare is rupees 783 find its base and height   
Asked by yuvrajlkr8877 | 07 Aug, 2019, 09:31: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
A piece of paper is in the shape of a right-angled triangle and is cut along a line that is parallel to the hypotenuse, leaving a smaller triangle. There was 35% reduction in the length of the hypotenuse of the triangle. If the area of the original triangle was 34 square inches before the cut, what is the area (in square inches) of the smaller triangle?
Asked by rushabhjain.av | 01 Apr, 2019, 07:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that a median divides a triangle into two triangle of equal area        
Asked by bhardwajvishesh2004 | 28 Nov, 2018, 04:18: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×